Ellipse in 1. Hauptlage sind eine Gleichung der Tangente t sowie der Berührungspunkt P gegeben. Gleichung der Ellipse!

Question

Aufgabe:

t:4x+5y=13, P(p_1|1)

Problem/Ansatz:

 y-Wert vom Punkt p in die Tangentengleichung , x=2!

Aber ich komme nicht weiter... Die ell in 1.Hautplage lautet wie bekannt: b^2x^2+a^2y^2=a^2b^2. Abér wie kann ich a^2 und b^2 ermitteln?

Lt Lösungsheft P(2|1) und ell: 2x^2+5y^2=13 heraus.

Ich bin für jede Hilfe äußerst dankbar.

Vielen Dank,

Lg.

Answer 1

Du musst vermutlich die Tangentensteigung ausrechnen und mit der Ableitung der Ellipsen-Funktion gleichsetzen. Dann noch die Koordinaten von P in die Ellipsengleichung einsetzen und du bekommst zwei Gleichungen mit zwei Unbekannten.

Comments

Vielen Dank!

Answer 2

Hallo

 ich schreibe lieber x^2/a^2+y^2/b^2=1 und die Gerade 4/13*x+5/13*y=1

dann die Tangentengleichung x*x_T/a^2+y*y_T/b^2=1 (x_T,y_T) einsetzen

2/a^2*x+1/b^2*y=1 also 4/13=2/a^2, 5/13=1/b^2

Gruß lul

Comments

Vielen Dank!

Answer 3

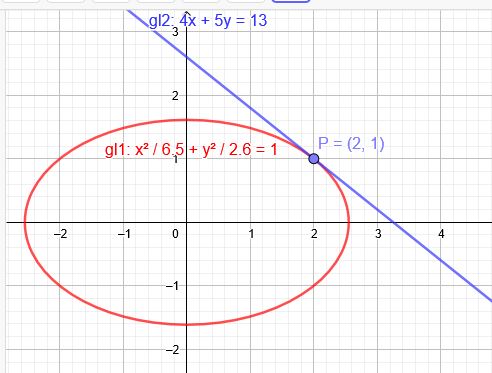
\(t:4x+5y=13, P(\red{2}|\blue{1})\)  Tangentensteigung \(m=\orange{-\frac{4}{5}}\) 

Ellipse:\(f(x,y)=b^2x^2+a^2y^2-a^2b^2\)

Ableitungen:

\(f_x(x,y)=2b^2x\)

\(f_y(x,y)=2a^2y\)

\(f'(x)=-\frac{f_x(x,y)}{f_y(x,y)} \)

\(f'(x)=-\frac{2b^2x}{2a^2y} =-\frac{b^2x}{a^2y} \)

\(f'(\red{2}) =-\frac{b^2 \cdot \red{2}}{a^2 \cdot \blue{1}} \)

\(f'(\red{2}) =\orange{-\frac{4}{5}} \)

\(-\frac{b^2 \cdot \red{2}}{a^2 \cdot \blue{1}}=\orange{-\frac{4}{5}} \)

\(b^2=\frac{2}{5}a^2=0,4a^2 \)    

\(P(\red{2}|\blue{1})\) liegt auf der Ellipse  \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\):

\(\frac{4}{a^2}+\frac{1}{b^2}=1\):  \(b^2=0,4a^2 \) einsetzen:

\(\frac{4}{a^2}+\frac{1}{0,4a^2}=1\)     \(a^2=6,5\)      \(b^2=0,4\cdot 6,5=2,6 \)

Ellipse: \(\frac{x^2}{6,5}+\frac{y^2}{2,6}=1\)