Aufgabe:
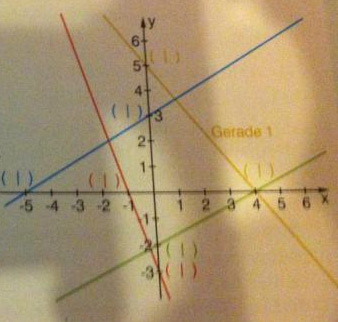
Markante Punkte nutzen.
a) Schreibe die Schnittpunkte der Geraden 1 mit den Koordinatenachsen auf und ermittle damit die zugehörige lineare Gleichung.
b) Überprüfe, ob die Gerade 1 die Lösungen der Gleichung \( \frac{x}{4}+\frac{y}{5}=1 \) darstellt. Diese Form der Gleichung nennt man Achsenabschnittsform.
c) Kannst du erklären, woher der Name "Achsenabschnittsform" kommt?
d) Stelle für die anderen Geraden auch die Achsenabschnittsform auf.