Hallo Marie,
Die Aufgabe setzt voraus, dass Kanten des Würfels auf drei Koordinatenachsen liegen. Ansonsten gäbe es 'viele' Lösungen!
Es reicht zunächst aus, den Würfel und die 5 Punkte zu zeichnen (z.B. im Schrägbild). Alle Punkte die nach dem Abschneiden der Ecken auf Kanten des neuen Körpers liegen, müssen auf der Oberfläche des Würfels liegen, aber nicht auf seinen Kanten, da diese abgeschnitten werden (ausgenommen die Kantemitten). Damit fallen die Punkte \(P_2\) und \(P_3\) bereits raus.
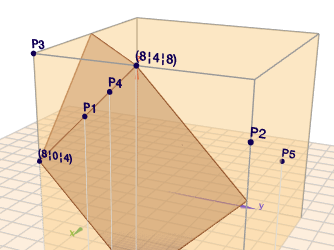
(klick auf das Bild und rotiere es mit der Maus)
Der Punkt \(P_5\) liegt genau mittig auf einer Fläche, also wird er auch auf keiner der zukünftigen Kanten liegen.
Bleiben die Punkte \(P_1\) und \(P_4\). Zeige, dass sich die beiden Punkte auf der Strecke zwischen den angrenzenden Kantenmitten des Würfels befinden.