VFortsetzung
Titel: Ebenen, Vektoren, Geraden, Schatten
Stichworte: vektoren,ebene,vektorgeometrie,analytische-geometrie
komme nochmals bei Teilaufgaben dieser Aufgabe nicht weiter, könnte mir jemand erklären, wie ich hier vorzugehen habe?
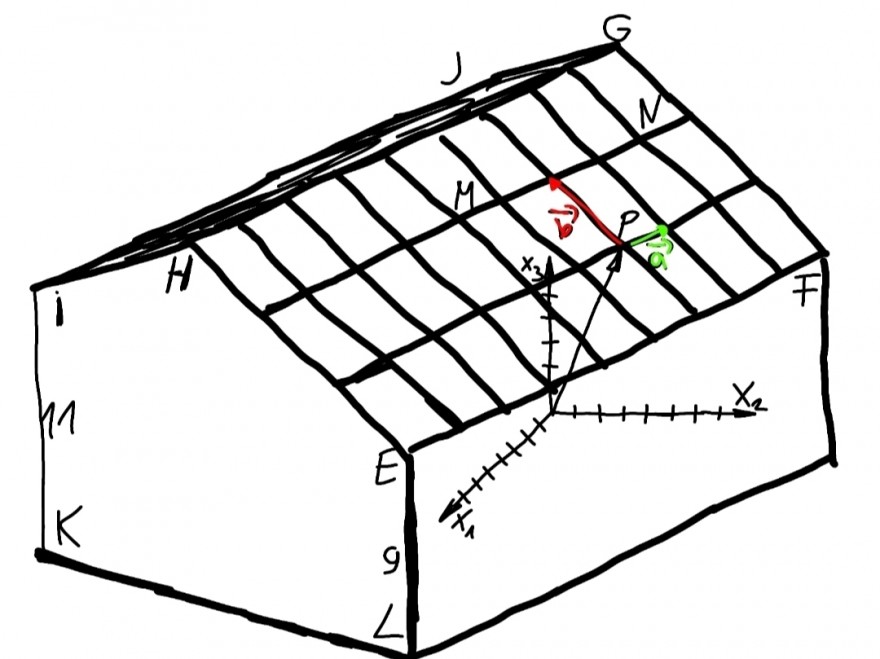
Nach meinen Berechnungen sind die Koordinaten der Punkte: P(8|7|11);I(12|-15|11);E(22|5|9), F(4|14|9), G(-2|2|15), H(16|-7|15).;M(10|1|13)
e) Der Mast soll im Punkt R durch ein Seil, welches durch den Dachboden gelegt wird, gegen heftigen Wind gesichert werden. Das Seil wird durch diese Gerade beschrieben:
h: \( \vec{x} \) = \( \begin{pmatrix} 10\\1\\3 \end{pmatrix} \) + r \( \begin{pmatrix} -2\\-9\\0 \end{pmatrix} \).
Berechne, an welchem Punkt S der Fläche IHGJ das Seil gelegt wird.
und
f) Dieser Mast ist 8m hoch. Berechne die Länge des Schattens, den der Mast auf die Fläche EFGH wirft, wenn die Strahlen entlang dem Vektor:
\( \vec{t} \) = \( \begin{pmatrix} 0\\1\\-2 \end{pmatrix} \) einfallen.
Könntet ihr mir sagen, wie ich hier vorgehe?
Vielen Dank schonmal! :)