Hallo,
zunächst zum Euler-Verfahren.
Stell Dir einen Topf mit heißem Wasser in der Küche vor. Der Topf steht auf dem Küchentisch und kühlt langsam auf die Zimmertemperatur der Küche runter. Angenommen die Temperatur \(\vartheta\) des Topfes beträgt zum Zeitpunkt \(t=0\) \(\vartheta(t=0)=70°\) und die Umgebungstemperatur in der Küche \(\vartheta_u=22°\) ist konstant. Der Wärmeverlust des Topfes an die Küche ist proportional der Temperaturdifferenz \(\vartheta-\vartheta_u\) mit dem Faktor \(k=0,01 \text{min}^{-1}\). So kann man die Differenzialgleichung aufstellen (Anfangswertproblem)$$\begin{aligned} \dot \vartheta &= -k(\vartheta - \vartheta_u) \\ \dot \vartheta &= - \frac 1{100 \,\text{min}} \left( \vartheta - 22°\right), \quad \vartheta(0) = 70°\end{aligned}$$mit der bekannten Lösung$$\vartheta = (70°-22°) \cdot e^{-0,01 \text{min}^{-1} \cdot t } + 22°$$Falls man nun nicht so einfach zur Lösung kommt, kann man auch das Eulerverfahren benutzen.
Zunächst wählt man ein kleines - dem Problem angemessenes - \(\Delta t\). Hier z.B.: \(\Delta t = 0,5 \text{min}\). Man geht also davon aus, dass sich die Zustände (hier die Temperatur) in 0,5min nicht wesentlich ändern. Dann berechnen man die Zustandsänderung - also das \(\dot \vartheta\) - in Abhängigkeit des Zustandes (der Temperatur) zum aktuellen Zeitpunkt. Heißt$$\dot \vartheta(t=0) = - \frac 1{100 \,\text{min}} \left( 70° - 22°\right) = -0,48 °C \text{min}^{-1}$$
Und da wir angenommen haben, dass sich in unseren Zeitintervall \(\Delta t\) nicht so viel ändern, kann man nun auf die Temperatur \(\vartheta_1\) am Ende dieses Zeitintervals schließen.
$$\begin{aligned} \vartheta_1 &= \vartheta_0 + \dot \vartheta(t=0) \cdot \Delta t \\&= 70° + (-0,48 °C \text{min}^{-1}) \cdot 0,5 \text{min} \\&= 69,76° \end{aligned} $$
Und mit dem neuen Zustand \(\vartheta_1\) berechnet man wieder die Zustands(Temperatur)änderung und daraus wieder den Folgezustand - usw. allgemein$$\vartheta_{i+1} = \vartheta_i + \dot \vartheta_i \cdot \Delta t$$ nach 100min - entsprechen 200 Iterationen - würde man eine Tempeartur von \(39,61°\) errechnen. Nach der theoretischen Lösung müssten es \(39,66°\) sein. Die Kurve sähe so aus
~plot~ 48*e^(-x/100)+22;[[-2|105|-2|75]];22 ~plot~
wenn man die berechnete Kurve ebenso einzeichnen würde könnte man beide nicht unterscheiden. Du siehst also, dass man den Verlauf der Kurve mit diesem Verfahren recht gut treffen kann.
Im mehrdimensionale Fall - hier in Deinem Beispiel mit Beute und Räuber - ändern sich nicht viel, außer, dass man eben zwei, statt einem Zustand berechnen muss. Die DGL lautet (in Vektorschreibweise)$$ \dot z = \begin{pmatrix} \dot x\\ \dot y\end{pmatrix} = \begin{pmatrix} f_x(x,y)\\ f_y(x,y) \end{pmatrix} = \begin{pmatrix} \alpha x - \beta xy\\ \delta xy - \gamma y \end{pmatrix}$$Ist der Zustand \(z_0 = (x(0)=1;\,y(0)=1)\) am Anfang gegeben, kann man nun mit einem gewählten \(\Delta t\) den Folgezustand \(z_1\) berechen$$z_1 = z_0 + \dot z_0 \cdot \Delta t$$und jeden weiteren auf Basis des vorhergehenden$$z_{i+1} = z_i + \dot z_i \cdot \Delta t$$In Deinem Fall soll nun sein$$ \dot z = \begin{pmatrix} x - xy\\ xy -y\end{pmatrix} $$Daraus folgt $$\dot z(t=0) = \begin{pmatrix} 1 - 1 \cdot 1\\ 1 \cdot 1 -1\end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix}$$D.h. dieser Zustand ist stabil - unabhängig von einem gewählten \(\Delta t\)!
Deshalb habe ich mal als Anfangswert \(z=(x=2;\, y=1)\) gewählt:
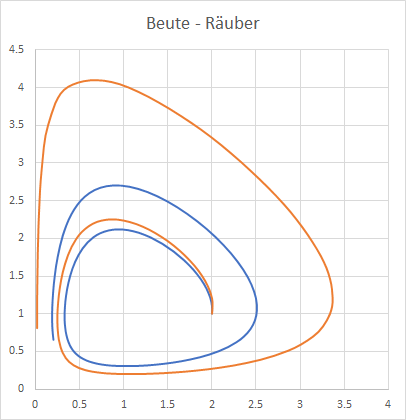
oben siehst Du das Resultat für ein \(\Delta t = 0,1\) (blau) und für ein \(\Delta t= 0,2\) in orange. Der Graph geht über einen Zeitraum von \(t=10\).
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner