Finde im Internet keine App/ Programme.

Question

Finde im Internet keine App/ Programme.

2 Antworten

In GeoGebra, ja...

Ich hab die Polarkoordinaten der Punkte/Vektoren in Listen abgelegt:

z_1={a,k}

z_2=z_1²={z_1(1)², z_1(2) + z_1(2)}

und damit weitergerechnet

Vektormultiplikation:={Multplikation des Modulus, Addition des Winkels}

und dann in GGB-Polarkoordinaten (a ; t) gewandelt zur Darstellung:

Das Polynom (3+3i) z³ + 2 z²

p(t)=(3sqrt(2) a³ ; 3t + 1 / 4 π) + (2a² ; t)

===>

$Curve\left(3 \; a^{3} \; \sqrt{2} \; \operatorname{cos} \left( 3 \; t + \frac{1}{4} \; \pi \right) + 2 \; a^{2} \; \operatorname{cos} \left( 2 \; t \right), 3 \; a^{3} \; \sqrt{2} \; \operatorname{sin} \left( 3 \; t + \frac{1}{4} \; \pi \right) + 2 \; a^{2} \; \operatorname{sin} \left( 2 \; t \right),t,0,2\pi \right)$

Ich lade das Beispiel hoch, da kannst Du es Dir abholen

https://www.geogebra.org/m/xaekmgkn

ACHTUNG: GGB-Polarkoordinaten haben einen Strichpunkt als Koordinatentrennzeichen! den Slider k als Animation starten zeichnet die Kurve...

Kommentiert 21 Aug 2020 von wächter

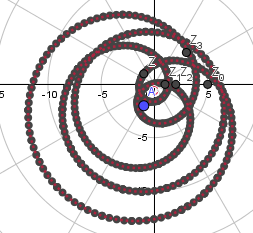
Das mußt Du Dir zusammenstellen, siehe im CAS

z=z_1={a,k} ===zeichnen===> Z_1=(a ; k)

z²=z_2={a*a, 2k) Z_2=(a² ;2 k)

Konstante q = c + b i in Polarkoordinaten wandeln

===> q = (r ; phi) ==übertrag==> {r , phi} und wie oben rechnen

q z³=z_3={r a³ , 3k+phi} Z_3=(r*a³ ; 3k+phi)

alle Summanden in Listenform bestimmen

p(z)=q z³+z²+z ====berechnen in Polarkoordinaten ===> Z_3 + Z_2 + Z_1

(k in der app) zur Animation von 0 ... 2pi laufen lassen

muß ggb überlisten die complexen Zahlen über Polarkoordinaten zur rechnen - intern läuft alles über kartesische Koordinaten.

r(z) = (3+3i)z³ + 2z² - 5z + (2-i)

PCURVE:=(3sqrt(2) a³; 3t + 1 / 4 π) + (2a²; 2t) - (5a;5t) + (sqrt(2²+1);pi+tan⁻¹(2))

t gegen k tauschen wenn ein Punkt über Slider k laufen soll

Kommentiert 21 Aug 2020 von wächter

Hm,

ich bevorzuge die alte 5.x auf einem Desktop ist 6.x auch IO, aber für meinen Geschmack zu eigensinnig im Handling.

Ich glaub jetzt hab ich's - hab eine Alternative am Bug vorbei gefunden - denk ich jetzt mal. Ich teste die Weitz-Beispiele. So weit ich verstanden hab, zieht er den Modulus so weit auf, dass der Ursprung "frei liegt" und schrumpft den Graph soweit ein bis er einen Schnitt mit dem Ursprung hat - den Winkel (k) draufstellen und Lösung ablesen.

---Der Abschnitt ist mir noch nicht so klar - vielleicht kannst Du was dazu sagen?

The main point here is that we can make |z| so large that the curve through which p(z) passes will always be outside a circular disk around zero, no matter how p(z) looks. And we can make the disk as large as we want. (There's even a simple formula which tells you algebraically how large |z| has to be depending on the coefficients of p(z), but I'll refrain from showing it here.)

---

Die Formel würde mich interessieren...

Ist das so weit der Plan?

Beispiel an einer selbstgewählten Funktion

Die Funktion gefällt mir wegen der Brezel :-)...

Wie würde meine Arbeit, wenn ist fertig ist (ich muss noch den Quadranten berücksichtigen um den Winkel korrekt angeben zu können), denn in Deiner wissenschaftlichen Arbeit zum Tragen kommen?

Kommentiert 23 Aug 2020 von wächter

Erstmal vielen Dank für dein Engagement. So wie ich des verstehe will er in dem Absatz aussagen, dass man eben z so gros wählen kann das die Figur eben sehr weit weg vom Nullpunkt liegt. Zur Verdeutlichung bezieht er halt noch diese Scheibe in der Mitte mit ein, dass man sieht das für große z die scheiben nicht geschnitten wird.

Meines erachtens will er einfach verdeutlichen wie weit weg die Figur vom Nullpunkt ist und sie dann doch plötzlich für gewisse Werte ihn schneidet.

genau weiß ichs noch nicht wie ich es einbringe. Aber in der arbeit wahrscheinlich 2 Bilder. Einmal so wie jetzt grade wenn es schneidet und des andere ganz am Anfang. Vor Allem hilft mir diese Animation in meiner Präsentation, wo ich sie einfach ablaufen kann.

Wenn ,man dein Beispiel vergrösern und verkleinern kann, wäre des dann perfekt:)))))

Welche Formel würde dich interessieren?? Versteh net ganz was du meinst.

lg

Kommentiert 23 Aug 2020 von Hanspeter12

---

There's even a simple formula which tells you algebraically how large |z| has to be depending on the coefficients of p(z)

Sehr weit weg ist jetzt net unbedingt mathematisch fassbar;-).

Nun, wenn Du Dir mein Polynom anschaust, dann bewegt sich der Realteil der Nullstellen zwischen ~1.5 - 0.32 - das Vorzeichen erscheint im Winkel (da hab ich Probleme den Winkel richtig abzulesen entsprechend dem Quadranten) also muss Du a über 1.5 aufziehen, um diese Nullstelle beim Schrumpfen zu erreichen. Deshalb wäre og. Formel interessant.

Da diese Darstellung auf einer Vektorkette basiert findet man eine Nullstellen wenn die Vektorkette der Kooeffizienten geschlossen wird - also in den Ursprung zurückkehrt -blaue Pfeile Z_i)

Und nochmal:

Wie würde meine Arbeit, wenn sie fertig ist, denn in Deiner wissenschaftlichen Arbeit zum Tragen kommen?

Kommentiert 23 Aug 2020 von wächter