Welchen Flächeninhalt hat das Viereck PBCD?

Question

Im Inneren des Quadrates ABCD liegt ein Punkt P, der von D den Abstand 1, von A den Abstand 2 und von B den Abstand 3 hat. Welchen Flächeninhalt hat das Viereck PBCD?

Comments

@Roland

Denkst du dir deine Geometrie-Aufgaben eigentlich selbst aus oder sind das Aufgaben, die man irgendwo einsehen kann? Ich beschäftige mich gerade ein bisschen mit ebener Geometrie, da ich dort noch viel zu lernen habe...

Ich bin auf der Suche nach Material, an denen man etwas experimentieren kann.

Answer 1

Hallo Roland,

das ist jetzt nicht soooo schwer ...

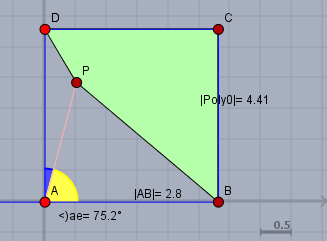
... stelle den Cosinussatz für die Dreiecke \(\triangle ABP\) und \(\triangle APD\) auf, jeweils mit dem Winkel \(\alpha\) (gelb) bei \(A\):$$3^2 = a^2 + 2^2 - 4a \cos \alpha \\ 1^2 = a^2 + 2^2 - 4a \cos \left( \frac \pi 2 - \alpha\right) $$\(a\) sei die Seitenlänge des Quadrats. Dann Additionstheorem anwenden, trigonometrische Funktion auf eine Seite der Gleichung isolieren, das ganze quadrieren und addieren, damit \(\alpha\) raus fällt, und raus kommt für \(a\)$$a = \sqrt{5 + 2\sqrt2}$$Jetzt kommt der aufwendigere Teil, nämlich nach der Formel von Heron die Flächen der beiden oben erwähnte Dreiecke berechnen. Das habe ich mir einfach gespart, und es nummerisch berechnet. Und aus der nummerischen Lösung \(F_{PBCD} \approx 4,4142\) und ein wenig Erfahrung mit Zahlen ;-) komme ich auf:$$F_{PBCD} = 3 + \sqrt 2$$

Die 'geniale' Lösung:

Man drehe das Dreieck \(\triangle APD\) um \(90°\) nach rechts in das Dreieck \(\triangle AP^*B\). Dann ist der Winkel \(\angle P^*AP\) ein rechter und damit die Strecke \(|PP^*| = 2 \sqrt 2\). Und da \(|PB|=3\) und \(|P^*B|=1\) ist, ist der Winkel \(\angle BP^*P\) ebenso ein rechter.

 

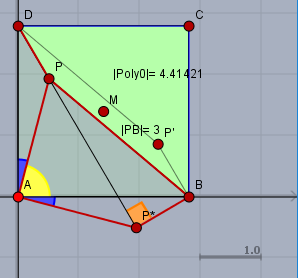
Die Fläche des Vierecks \(AP^*BP\) ist somit$$F_{AP^*BP} = 2 + \sqrt 2= F_{ABPD}$$Wenn man jetzt zeigen kann, dass sich die Flächen der beiden Vierecke \(ABPD\) und \(PBCD\) genau um \(1\) unterscheiden (das überlasse ich dem werten Leser - man beachte \(P'\)!), dann ist$$F_{PBCD} = F_{ABPD} + 1 = 3 + \sqrt 2$$

Comments

Deine (aus Erfahrung mit Zahlen) gewonnene Lösung ist (vielleicht zufällig) richtig. Das Ganze geht aber auch zuverlässiger - entweder durch eine geniale Idee oder durch aufwändige Rechnung. Deine vorangestellte Behauptung "das ist jetzt nicht soooo schwer ..." gilt also nur für deinen Lösungweg, den ich im Bereich des Ratens ansiedle.

---

Also \(|CB|=|DC|= \sqrt{5 + 2\sqrt2}\), \(|BP|=3\) und \(|DP|=1\). Nun kann man z. B. die Formel von Bretschneider anwenden.

---

... entweder durch eine geniale Idee ..

geniale Lösungen dauern immer etwas länger (s.o.) ich habe die Antwort erweitert.

---

Nun kann man z. B. die Formel von Bretschneider anwenden.

das ist ja noch schlimmer, als die von Heron. Setze doch da mal das \(a=\sqrt{5+2\sqrt2}\) für eine der Seiten ein. Das wird doch eine furchtbare Wurzelei.

Da bin ich jetzt zu alt für. Ich habe nicht mehr so viel Zeit!

---

Bretschneider ist das Pendant zu Heron fürs Viereck. Ich rechne so oder so mit einem Programm. Damit brauche ich für die Eingabe max. 2 min.

Answer 2

Der Ursprung des Koordinatensystems liege bei A.

Der Punkt P habe die Koordinaten x und y, die Seitenlänge des Quadrats sei z.

x^2+y^2=4

(z-y)^2+x^2=1

(z-x)^2+y^2=9

Der gesuchte Flächeninhalt ist

A=z^2-0,5z(x+y)

Die Gleichungen haben mehrere Lösungen, von denen positive Werte interessieren:

Mit Wolframalpha finde ich:

\( A \approx 4.41421, \quad x \approx 0.505449, \quad y \approx 1.93508, \quad z \approx 2.79793 \)

Der Flächeninhalt des Quadrats ist übrigens \( z^{2}=5+2 \sqrt{2} \).

Comments

Das war auch mein Ansatz, doch von Hand habe ich mich immer wieder verzettelt.

Ich frage mich, wie Leibniz und Co das ohne diesen Wolfram gemacht haben.

Oder Gauß oder Bessel, einer von denen, hätte das bestimmt gekonnt.

---

... und es gab ja noch nicht einmal Taschenrechner!

Ich hatte meinen ersten übrigens im 3. Semester gekauft, das war 1975. Der konnte weniger als heutzutage ein 10 Euro-Rechner, hat allerdings 250DM gekostet. (Eine Woche vorher war der Preis noch bei 500DM!) Trotzdem war er im Vergleich zu Rechenschieber und Logarithmentafel eine enorme Erleichterung.

:-)

---

Ja, 1974 hatten die meisten bei uns in der Vermessung den HP 45  der hatte 1000 DM gekostet, Das Geld konnte und wollte ich nicht ausgeben, dafür musste ich die Rechenwege aber immer übersetzen da die Eingabe beim HP eine etwas andere war. Im Vergleich zu heute, konnte der auch nicht viel, hatte aber mehrere Speicher. Aber immerhin, ich durfte in der Ausbildung noch mit Tafel und Kurbelrechenmaschine arbeiten.

Wenn wir am der FH größere Rechnungen gemacht haben, mussten wir diese immer auf Lochstreifen im Rechenzentrum abgeben, 14 Tage später kam dann das Ergebnis. Häufig stand da ein Syntax Error, manchmal auch, weil die Löcher nicht richtig gestanzt worden waren.

---

PDP-10

..............

:-)

---

Puh, jetzt habe ich es auch von Hand geschafft.

Die Subtraktion der von Monty Python erwähnten Gleichungen führte zu

2zy = z²+3. und 2zx = z² -5

und eingesetzt in  x² + y² =4

zu  z^4 - 10z² + 17 = 0

was zur mittlerweile bekannten Formel führt.

z² = 5 + 2\( \sqrt{2} \)

Nachzutragen bleibt, dass

y= \( \frac{4 + \sqrt{2}}{z} \).

x= \( \frac{ \sqrt{2}}{z} \)

der Mittagsschlaf hat geholfen.

Damit ist mit

A= z² - 0,5 (xz+yz)

A= 3 + \( \sqrt{2} \)

Eigentlich war es nicht schwierig, doch es gab reichlich Gelegenheiten Fehler zu machen.

---

@Hogar

Pluspunkt für deinen Kommentar!

:-)