Bestimmen Sie den Punkt auf dem Paraboloid mit geringsten Abstand

Question

Aufgabe:

Bestimmen Sie den Punkt auf dem Paraboloid
$$x^{2}+y^{2}=2 z+9$$
der vom Punkt $P(4,6,1)$ den geringsten Abstand hat.
Hinweis: Zur Vereinfachung minimieren Sie statt des Abstands $d(x, y, z)$ die Funktion $d^{2}(x, y, z)$

Vielen Dank

Comments

Hallo

du kannst doch sicher den Abstand d zu einem beliebigen Punkt des Paraboloids bestimmen? Statt dann die Wurzel zum Min zu machen einfach d² minimieren,

wo genau liegen deine Schwierigkeiten ?

lul

Answer 1

Wo liegen konkret die Probleme

Hier zunächst eine Kontroll-Lösung von Wolframalpha

Es handelt sich hier um eine Minimierung unter einer Nebenbedingung. Könnte man z.B. mit Lagrange machen denke ich.

Answer 2

Hallo,

Die Aufgabe besagt eine Punkt $Q$ zu finden, der zu $P$ einen möglichst kleinen Abstand hat. Formal $$|Q - P| \to \min$$ oder einfacher, weil ohne Wurzel $$(Q-P)^2 \to \min$$mit dem konkreten $P(4|\,6|\,1)$ und $Q(x|\,y|\,z)$ ist die Funktion $d^2$ des Quadrats des Abstands nebst der Nebenbedingung, dass sich $Q$ auf dem Paraboloiden befinden muss$$d^2(x,y,z) = (x-4)^2+ (y-6)^2 + (z-1)^2 \to \min \\ \text{NB:} \space x^{2}+y^{2} -2 z-9 = 0$$zu minimieren. Die Lagrange-Funktion nebst Ableitungen sind dann $$L(x,y,z,\lambda) =(x-4)^2+ (y-6)^2 + (z-1)^2 + \lambda(x^{2}+y^{2} -2 z-9) \\ \frac{\partial L}{\partial x} = 2(x-4) + 2x\lambda = 0 \\ \frac{\partial L}{\partial y} = 2(y-6) + 2y\lambda = 0 \\ \frac{\partial L}{\partial z} = 2(z-1) - 2\lambda = 0 \implies \lambda = z-1$$aus der letzten folgt ein $\lambda$ welches man in die beiden anderen einsetzen kann und am Ende kann man das vereinfachen zu $$-3x + 2y = 0$$was absolut Sinn macht. Das ist nämlich die hellgrüne Ebene hier

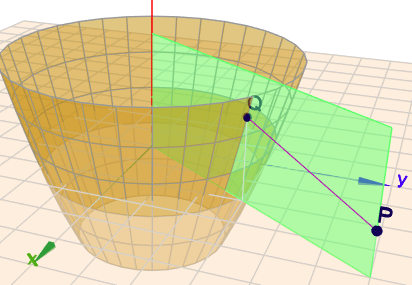
das ganze ist ja rotationssymmetrisch bezüglich der Z-Achse. Wenn man das rückwärts in die Nebenbedingung einsetzt, so kommt man das auf das $Q=(2|3|2)$.

klick auf das Bild und wenn Du noch Frage hast, so melde Dich bitte.