Ich habe die Aufgabe mal unter folgendem Link bearbeitet:
https://docs.google.com/document/d/1EdQjk7bRak0eHcynjM0uClY_9ZbCeRaQZdjJjI1zWYk/pub
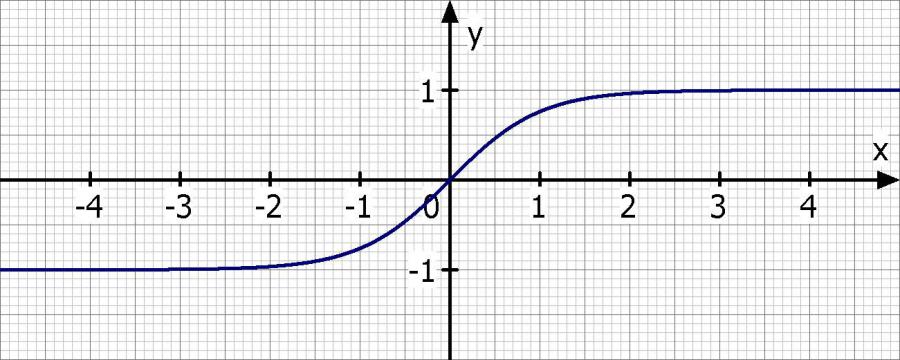
Kurvendiskussion: f(x) = tanh(x)
Funktion
f(x) = tanh(x) = (e^x - e^{-x}) / (e^x + e^{-x}) = (e^{2·x} - 1)/(e^{2·x} + 1)
(i) maximalen Definitionsbereich finden.
D = R
Der Nenner darf nur nicht 0 werden. Da die e-Funktion aber immer > 0 ist, kann der Nenner hier nie null werden.
(ii) Symmetrieeigenschaften der Funktion untersuchen.
f(-x) = (e^{-x} - e^x) / (e^{-x} + e^x) = -(e^x - e^{-x}) / (e^x + e^{-x}) = - f(x)
Hier liegt eine Punktsymmetrie vor
(iii) Nullstellen berechnen.
(e^x - e^{-x}) = 0
e^x - 1/e^x = 0
e^{2·x} - 1 = 0
e^{2·x} = 1
x = 0
(iv) Grenzwerte für x → ± ∞ berechnen.
lim (x → ∞) (e^x - e^{-x}) / (e^x + e^{-x}) = 1
lim (x → -∞) (e^x - e^{-x}) / (e^x + e^{-x}) = -1
(v) maximalen Monotoniebereiche angeben
f(x) = (e^{2·x} - 1)/(e^{2·x} + 1)
f'(x) = 4·e^{2·x}/(e^{2·x} + 1)^2
Zähler und Nenner sind immer positiv. Dadurch ist die Funktion in ganz D monoton steigend.
(vi) Extrema finden.
f'(x) = 4·e^{2·x}/(e^{2·x} + 1)^2 = 0
Der Zähler wird nicht 0. Damit gibt es keine lokalen Extrema. Globale Extrema an die sich die Funktion annähert sind danach die Grenzwerte -1 und 1.
(vii) Handelt es sich bei diesen um Maxima oder Minima? Welche Extrema sind lokal, welche global?
Der Grenzwert -1 ist ein Minimum der Grenzwert 1 ist ein Maximum.
(viii) Wendepunkte sowie maximale Bereiche, in denen der Graph konkav bzw. konvex ist berechnen.
f''(x) = 8·e^{2·x}·(1 - e^{2·x})/(e^{2·x} + 1)^3 = 0
1 - e^{2·x} = 0
e^{2·x} = 1
x = 0
Wendepunkt W(0, 0)
Für x > 0 ist die Funktion konkav
Für x < 0 ist die Funktion konvex
(ix) Anfertigung einer Skizze der Funktion mit Hilfe der bereits berechneten charakteristischen Punkte, ohne weitere Werte (z.B. mit dem Taschenrechner).