Grenzwert bestimmen: limx→0 (1/x - 1/(x2)

Question

Aufgabe:

Grenzwert bestimmen:

$\lim \limits_{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{x^{2}}\right)$

Answer 1

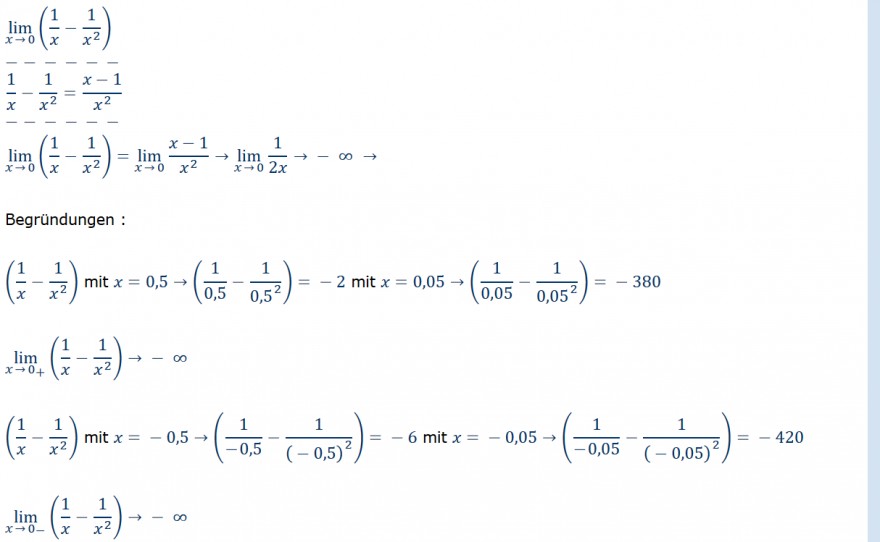
Text erkannt:

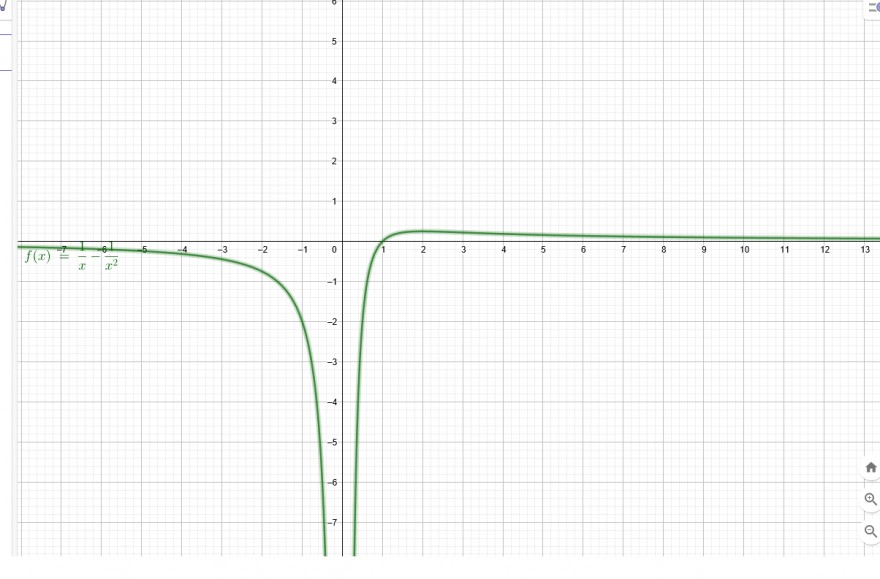
$\lim \limits_{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{x^{2}}\right)$
$\frac{1}{x}-\frac{1}{x^{2}}=\frac{x-1}{x^{2}}$
$------$
$\lim \limits_{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{x^{2}}\right)=\lim \limits_{x \rightarrow 0} \frac{x-1}{x^{2}} \rightarrow \lim \limits_{x \rightarrow 0} \frac{1}{2 x} \rightarrow-\infty \rightarrow$
Begründungen
$\left(\frac{1}{x}-\frac{1}{x^{2}}\right)$ mit $x=0,5 \rightarrow\left(\frac{1}{0,5}-\frac{1}{0,5^{2}}\right)=-2$ mit $x=0,05 \rightarrow\left(\frac{1}{0,05}-\frac{1}{0,05^{2}}\right)=-380$
$\lim \limits_{x \rightarrow 0_{+}}\left(\frac{1}{x}-\frac{1}{x^{2}}\right) \rightarrow-\infty$
$\left(\frac{1}{x}-\frac{1}{x^{2}}\right)$ mit $x=-0,5 \rightarrow\left(\frac{1}{-0,5}-\frac{1}{(-0,5)^{2}}\right)=-6$ mit $x=-0,05 \rightarrow\left(\frac{1}{-0,05}-\frac{1}{(-0,05)^{2}}\right)=-420$
$\lim \limits_{x \rightarrow 0-}\left(\frac{1}{x}-\frac{1}{x^{2}}\right) \rightarrow-\infty$

mfG

Moliets

Comments

Ich merke gerade, dass der Weg über Hospital nicht erlaubt ist.

Ich habe es daran gemerkt, dass bei lim _x->0  ja   ∞ rauskommt, aber der Graph gibt das ja nicht her. Folgerung : Aufpassen ob Hospital auch angewandt werden darf.

Aber nur mit den Begründungen erreiche ich die Werte → - ∞

mfG

Moliets

Answer 2

1/x -  1/x²  = (x-1)/ x² für x gegen 0 geht der Zähler gegen -1

und der Nenner gegen 0, also Grenzwert -∞.

Answer 3

1/x - 1/x²
x / x² - 1 / x²
( x -1 ) / x²
für lim x -> ± 0 [ ( x -1 ) / x² ]= -1 / 0 = - ∞