Bestimmen Sie die Taylorreihe fur die Funktion f(x) = ln(1 + x) um den Entwicklungspunkt ξ = 0 , und sqrt(e) mit der

Question

Aufgabe:

Bestimmen Sie die Taylorreihe fur die Funktion f(x) = ln(1 + x) um den Entwicklungspunkt ξ = 0 , und  sqrt(e)  mit der Genauigkeit 0,001.

Answer 1

Aloha :)

Die Summenformel für die unendliche geometrische Reihe lautet:$$\sum\limits_{k=0}^\infty x^k=\frac{1}{1-x}\quad;\quad |x|<1$$Setzen wir an Stelle von $x$ einfach $(-x)$ ein, erhalten wir:$$\sum\limits_{k=0}^\infty (-x)^k=\frac{1}{1-(-x)}=\frac{1}{1+x}\quad;\quad |x|<1$$Da die Konvergenz der Reihe für $|x|<1$ gesichert ist, können wir beide Seiten der Gleichung integrieren und in der Reihe alle Summanden einzeln integrieren:

$$\int\limits_0^x\sum\limits_{k=0}^\infty(-x')^k\,dx'=\int\limits_0^x\frac{1}{1+x'}\,dx'\quad\implies\quad\sum\limits_{k=0}^\infty\int\limits_0^x(-x')^k\,dx'=\left[\ln|1+x'|\right]_{x'=0}^x$$$$\ln(1+x)=\sum\limits_{k=0}^\infty-\frac{(-x)^{k+1}}{k+1}=\sum\limits_{k=1}^\infty-\frac{(-x)^{k}}{k}=\sum\limits_{k=1}^\infty(-1)^{k+1}\cdot\frac{x^{k}}{k}$$Damit ist die Potenzreihe klar.

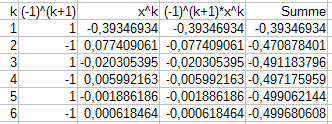
Nun sollen wir noch $\ln\sqrt e=\frac{1}{2}$ näherungsweise bestimmen. Dafür müssten wir $x=\sqrt e-1\approx1,718282$ setzen. Da dieses $x>1$ ist, konvergiert die Taylor-Reihe nicht. Daher rechnen wir wie folgt:

$$\ln(1+x)=\ln\left(\left(\frac{1}{1+x}\right)^{-1}\right)=-\ln\left(\frac{1}{1+x}\right)=-\ln\left(\frac{1+x-x}{1+x}\right)$$$$\phantom{\ln(1+x)}=-\ln\left(1-\frac{x}{1+x}\right)$$Wir rechnen also:$$\ln(\sqrt e)=\ln(1+(\sqrt e-1))=-\ln\left(1-\frac{\sqrt e-1}{1+(\sqrt e-1)}\right)$$$$\phantom{\ln(\sqrt e)}=-\ln(\,1+(-0,39346934)\,)$$Mit $x=-0,39346934$ erreichen wir die geforderte Genauigkeit bei $k=5$:

Comments

Hallo Tschakabumba,

Ich muss die selbe Aufgabe machen. Nur, dass mit der Aufgabenstellung gemeint war, dass man $\sqrt{e}$ bestimmen soll und nicht $ln(\sqrt{e})$.

Ich verstehe nicht ganz warum bei deiner Variation der Aufgabe -0,5 approximiert wird und nicht 0,5.

Wir haben bestimmt, dass unser $x=e^{\sqrt{e}}-1$

Und für das zweite x unten haben wir ungefähr 0,8077043545 heraus.

Die Taylorsumme nähert sich bei uns dem Wert 0,587 an, was nicht ansatzweise der wert von Wurzel e ist. Ich weiß nicht wirklich weiter.

---

Hier sollte $\sqrt e$ approximiert werden. Also musste ich das $x$ so wählen, dass:$$1+x=\sqrt e\implies x=\sqrt e-1\approx1,7818$$Das $x$ ist also größer als $1$. Die geometrische Reihe konvergiert aber nur für $|x|<1$ und nach der gezeigten Herleitung konvergiert dann auch $\ln(1+x)$ nur für $|x|<1$.

Also habe ich den Kehrwert approxmiert:$$\ln(1+x)=\ln\left(\left(\frac{1}{1+x}\right)^{-1}\right)=-\ln\left(\frac{1}{1+x}\right)$$Das Argument habe ich dann noch umgeschrieben:$$\frac{1}{1+x}=\frac{1+x-x}{1+x}=\frac{1+x}{1+x}-\frac{x}{1+x}=1-\frac{x}{1+x}$$um die gezeigte Näherungsformel verwenden zu können, denn jetzt kann ich$$x'=-\frac{x}{1+x}$$wählen, wobei $|x'|<1$ ist und die Reihe sicher konvergiert.

Dadurch dass ich den Kehrwert approximiere, kommt das Minuszeichen:$$\ln\left(\frac{1}{\sqrt e}\right)=-\ln(\sqrt e)$$

Ihr habt nun dasselbe Problem mit eurem Wert: $x=e^{\sqrt e}-1>1$. Daher konvergiert die Summe nicht. Benutze die Formel von hier:$$\ln(1+x)=-\ln\left(1-\frac{x}{1+x}\right)$$setze$$x'\coloneqq-\frac{x}{1+x}$$und nähere dann mit der hergeleiteten Formel. Du bekommst den exakten Wert, aber mit negativem Vorzeichen.

Answer 2

Hallo

wo liegt denn da die Schwierigkeit? die Ableitungen sind doch einfach? dann x=0 einsetzen in die Formel der taylorreihe.

sollst du wirklich damit ln(√e) bestimmen? ln(√e)=1/2*ln(e)=1/2  oder was bedeutet " und sqrt(e)  mit der Genauigkeit 0,001."?

Dazu müsstest du noch was sagen.

wenn du das wirklich mit dem Taylorpollynom sollt musst du ja zuerst √e-1=a kennen   um dann ln(a+1) auszurechen?

Gruss lul