Hallo,
A(3/2/1) B(3/6/1) C(-1/6/1) D(-1/2/1) E(3/2/5) F(3/6/5) G(-1/6/5) H(-1/2/5) S(3/5/6)
Kann mir bitte jemand was zu dem Ansatz sagen?
Ja - so wie die Punkte dort stehen sieht es so aus:
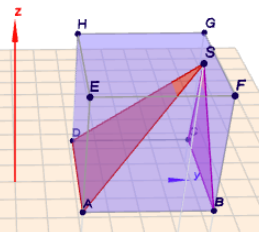
Der Punkt \(S\) liegt etwas neben der Mitte und auch nicht in der Ebene \(EFGH\). Klick auf das Bild und rotiere die Szene mit der Maus, dann wird es deutlich.
Der Punkt \(S\) muss in der Mitte zwischen den Punkten \(E\) und \(G\) oder auch \(F\) und \(H\) liegen.$$S = \frac 12(E + G) = \begin{pmatrix}1\\ 4\\ 5\end{pmatrix}$$
a) Bestimmen Sie die Größe des Winkels zwischen der Grundfläche und einer Seitenfläche der Pyramide.
Denke Dir die Pyramide parallel zur YZ-Ebene mittig aufgeschnitte. Man erhält folgendes Bild
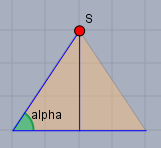
Der Tangens des Winkels \(\alpha\) (grün) zwischen der Seitenebene \(ASD\) und der Grundfläche ist das Verhältnis Höhe zu halber Grundseite. Und da das hier innerhalb eines Würfels ist, ist$$\tan \alpha = 2 \implies \alpha \approx 63,43°$$
b) Bestimmen Sie die Größe des Winkels zwischen benachbarten Seitenflächen der Pyramide.
Willst Du den Winkel zweier Ebenen zueinander berechnen, die nicht so offensichtlich sind wie bei a), so ist eine Methode, den Winkel der beiden Normalenvektoren zu bestimmen. Die Normalenvektoren \(\vec n_{ASD}\) und \(\vec n_{BSA}\) lassen sich aus dem Kreuzprodukt zweier Richtungsvektoren der Ebene bestimmen. Hier ist$$\vec n_{ASD} = \vec{DA} \times \vec{DS} = \begin{pmatrix}4\\ 0\\ 0\end{pmatrix} \times \begin{pmatrix}2\\ 2\\ 4\end{pmatrix} = \begin{pmatrix}0\\ -16\\ 8\end{pmatrix} \\ \vec n_{BSA} = \vec{AB} \times \vec{AS} = \begin{pmatrix}0\\ 4\\ 0\end{pmatrix} \times \begin{pmatrix}-2\\ 2\\ 4\end{pmatrix} = \begin{pmatrix}16\\ 0\\ 8\end{pmatrix}$$Und nun kann man mit dem Skalarprodukt den Winkel \(\varphi\) zwischen diesen beiden Vektoren berechnen. Es ist$$\cos \varphi = \frac{\vec{n}_{ASD} \cdot \vec{n}_{BSA}}{|\vec n_{ASD}|\cdot|\vec n_{BSA}|} \\\quad = \frac{16\cdot 0 +0 \cdot (-16) + 8\cdot 8}{\sqrt{0^2 + (-16)^2 + 8^2} \cdot \sqrt{16^2 + 0^2 + 8^2}} \\\quad = \frac{64}{320} = 0,2 \\ \implies \varphi \approx 78,46° $$diesen Winkel muss man noch von 180° abziehen. Warum das so ist, soll folgendes Bild klären:
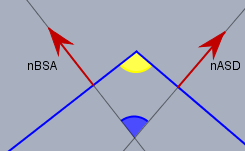
Die Ecke soll die Kante \(AS\) im Schnitt darstellen. Die blauen Strecken sind zwei Seitenflächen der Pyramide im Schnitt. Die beiden Normalenvektoren sind rot eingezeichnet. Der Winkel \(\varphi\) ist der WInkel zwischen den beiden Normalenvektoren, also der blaue Winkel. Der Winkel zwischen den Ebenen (gelb) ist \(180°-\varphi\), da die Winkelsumme im Viereck 360° ist, und die beiden verbleibenden Winkel rechte sind.
Ich habe das nochmal im Geoknecht3D eingegeben.
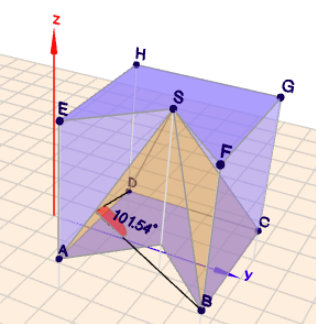
Würfel und Pyramide sind aufgeschnitten dargestellt, so dass man besser die 'Innereien' sehen kann. Falls etwas unklar ist, so frage bitte nach.