Wie konstruiere ich das Fünfeck?

Question

Aufgabe:

Konstruiere das Fünfeck ABCDE

ich habe ein Fünfeck in einer Mathe Aufgabe, und es sind 2 Seiten gegeben.

Also BC=CD=DE = 6cm und AB=AE = 5cm

Problem/Ansatz:

Wie konstruiere ich das Fünfeck?

Answer 1

Hallo Bella,

Die diagonal zwischen b und e ist 6cm
Ja die Punkte bei c und d sind Rechte Winkel
Ja und die Figur ist symmetrisch die durch a verläuft

zusammen mit der impliziten Annahme, dass die Figur konkav ist, reichen diese Informationen aus, um das Häuschen eindeutig zu konstruieren. Beginne unten auf dem Papier und zeichne waagerecht die Strecke $CD$ - Länge 6cm. Dann errichte in beiden Punkten $C$ und $D$ eine Senkrechte und trage wieder die Länge von 6cm nach oben ab.

Oberhalb von $C$ schneidet ein Kreis mit Durchmesser 6cm die Senkrechte im Punkt $B$ und oberhalb von $D$ im Punkt $E$. Zum Schluß schlage mit dem Zirkel je einem Kreis um $B$ und $E$ mit 5cm. Der obere von den beiden Schnittpunkten der Kreise ist der Punkt $A$.

Comments

Hallo Werner

ich bewundere deine Geduld und Kreativität, unvollständige Fragen  in einzelnen stenographischen Bemerkungen beantwortet , zu lösen.

an Bella: merkst du eigentlich wieviel Arbeit du machst mit ungenauen Angaben?

Gruß lul

---

@lul: Danke für das Kompliment.

an Bella: merkst du eigentlich wieviel Arbeit du machst mit ungenauen Angaben?

@lul: das sind Schüler, die müssen auch das erst lernen. Wie hj schon richtig angemerkt hat, wird da gleichseitig und gleichschenklig schnell verwechselt. Und dass es Vierecke gibt, wo kein Winkel ein rechter ist, das haben die vielleicht noch nie gesehen.

---

Also Wie lang muss ich jetzt CD, CB, DE zeichnen ?

---

Also Wie lang muss ich jetzt CD, CB, DE zeichnen ?

So wie Du es selber schon geschrieben hast: Ich zitiere Dich:

Also BC=CD=DE = 6cm und AB=AE = 5cm

.. aus Deiner Frage oben.

---

@Werner ich bedanke mich mehrmals, sie wissen nicht wie glücklich ich bin. Da ich homeschooling habe ist es schwerer mit Aufgaben allein auszukommen. Ich habe alles verstanden. DANKE DANKE DANKE DANKE DANKE

---

@lul: ich habe gelernt, dass in der Mathematik gilt: wenn Du die Frage wirklich korrekt und lupenrein formulieren kannst, so ist das im Prinzip bereits die Lösung.

Und wenn Bella in der Lage gewesen wäre, die Figur eindeutig und zweifelsfrei zu beschreiben, so könnte sie sie auch zeichnen.

Mathematik besteht IMHO weniger darin, Antworten zu finden, sondern die richtigen Fragen exakt zu stellen.

---

Hallo, wie groß ist das Dreieck Alpha BAE Winkel also

---

Hallo, wie groß ist das Dreieck Alpha BAE Winkel also

Stellt sich zunächst mal die Frage: was ist ein "Dreieck Alpha BAE Winkel"? ;-)

Wir wissen nicht, ob es sich um eine Dreieck - bzw. seine Fläche - oder um einen Winkel handelt. Oder um was anderes.

Für die Fläche eines Dreiecks braucht man i.A. eine Grundseite und die Höhe, die senkrecht darauf steht. Die Länge der Seite $BE$ ist bekannt. $|BE| = 6$.

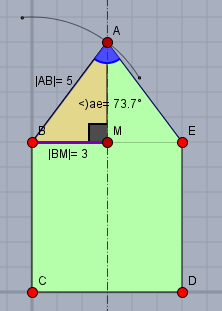
Die Höhe $AM$ lässt sich aus dem Dreieck $\triangle BMA$ berechnen (hellbraun). Dieses Dreieck ist rechtwinklig und folglich gilt nach Pythagoras$$|AM|^2 + |BM|^2 = |AB|^2, \quad |BM| = \frac 12|BE| = 3\\ \implies |AM| = \sqrt{|AB|^2- |BM|^2} = \sqrt{5^2 - 3^2} = 4$$Also ist die Fläche $F$ des Dreiecks $\triangle BEA$$$F = \frac 12 |BE| \cdot |AM| = \frac 12 \cdot 6 \cdot 4 = 12$$

Winkel sind etwas schwieriger. Hier hilft wieder das rechtwinklige Dreieck $\triangle BMA$. Sei der blau markierte Winkel $\alpha = \angle BAE$, dann gilt für den halben Winkel im Dreieck $\triangle BMA$$$\sin \frac {\alpha}2 = \frac{|BM|}{|AB|} = \space \frac{\text{Gegenkathete}}{\text{Hypotenuse}} \\ \implies \alpha = 2 \arcsin\left( \frac{|BM|}{|AB|}\right) = 2 \arcsin\left( \frac 35 \right) \approx 73,7°$$Gruß Werner

Answer 2

Hallo

das geht nicht eindeutig , am einfachsten du konstruierst ein Dreieck also ein 5 Eck mit 2 entarteten Ecken  2 Seiten 5+6=11, eine Seite 6 . Oder verschweigst du eine Zusatzeigenschaft?

Gruß lul

Comments

Das Fünfeck besteht aus ein gleichseitiges Dreieck und einem Viereck.

---

... und einem Viereck.

Ist das Viereck ein Rechteck oder wenigstens ein symmetrisches Trapez? Oder irgendein komisches Viereck?

Die roten Seiten sind 5 und un die blauen 6cm lang

Sind die beiden 5cm-Seiten benachbart? Ist die Figur achsensymmmetrisch? Welche Kantenlänge hat das gleichseitige Dreieck?

---

Ein Viereck mit 4 gleich langen Seiten.

BC=CD=DE = 6cm sie gehören zum Viereck

Und Ab=Ae = 5cm gehören zum Dreieck

---

dann wären wir jetzt so weit:

fühlst Du Dich auch in der Lage, die anderen Fragen (s.o.) zu beantworten? Dann wird's genauer!

---

Ein Viereck mit 4 gleich langen Seiten.

das geht nicht, da eine Seite des Vierecks an das gleichseitige Dreieck grenzt und dieses hat lt. Deiner Aussage die Seitenlänge 5cm.

---

Ist die Größe des Winkel alpha 90graf? In dem Dreieck?

---

Ist die Größe des Winkel alpha 90graf? In dem Dreieck?

Hmm! - die Frage spricht Bände. Die Antwort ist: wenn das Dreieck ein gleichseitiges Dreieck ist, dann sind alle Winkel in diesem Dreieck gleich $60°$.

Ein gleichseitiges Dreieck ist ein Dreieck mit drei gleich langen Seiten.

Soll ich meine Fragen zu dem Fünfeck noch mal stellen oder findest Du sie oben wieder?

---

Können sie nochmal stellen

---

wenn das Dreieck ein gleichseitiges Dreieck ist

Aus Erfahrung weißt du doch sicher selbst, dass einerseits die Begriffe "gleichseitiges Dreieck" und "gleichschenkliges Dreieck" sowie andererseits die Begriffe "Viereck" und "Quadrat" häufig verwechselt oder synonym gebraucht werden.

---

Aus Erfahrung weißt du doch sicher selbst, dass einerseits die Begriffe "gleichseitiges Dreieck" und "gleichschenkliges Dreieck" sowie andererseits die Begriffe "Viereck" und "Quadrat" häufig verwechselt oder synonym gebraucht werden.

... aber sicher doch! ich hatte die Figur schon im Kopf.

Aber die Frage nach den 90° hatte mich wieder unsicher gemacht. Wenn Bella aber auch Dreieck als Synonym für Rechteck benutzt hat, dann macht es wieder Sinn.

---

Können sie nochmal stellen

Ist die Figur zu einer Achse symmetrisch, die durch den Punkt $A$ verläuft?

Sind die Winkel bei den Punkten $C$ und $D$ rechte Winkel?

Falls Nein - Ist die Diagonale zwischen $B$ und $E$ 5cm oder 6cm lang?

---

Die diagonal zwischen b und e ist 6cm

Ja die Punkte bei c und d sind Rechte Winkel

Ja und die Figur ist symmetrisch die durch a verläuft