Planfigur:
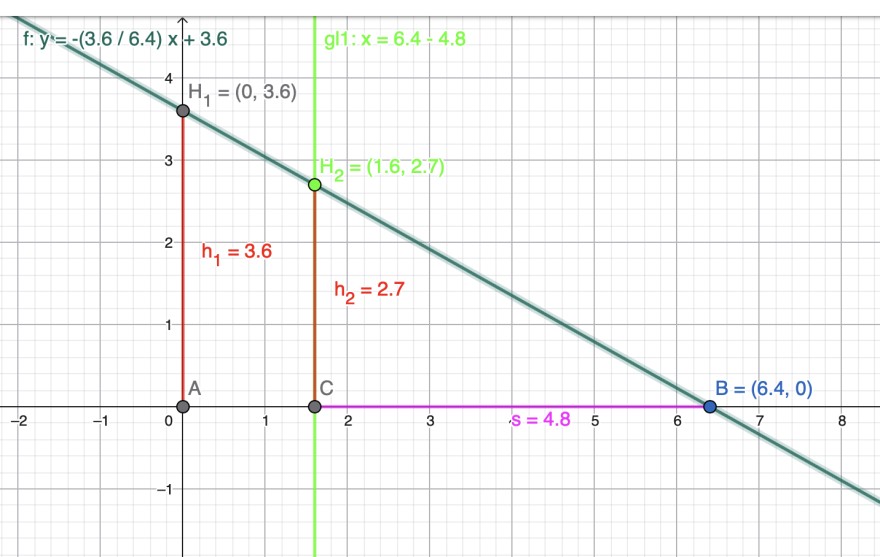
Zwei Bäume, die auf ein Grundstück stehen, werfen zur gleichen Zeit Schatten von 6,40 m und 4,80 m. Der größere Baum hat eine Höhe von 3,60 m.
Ich bestimme die Gleichung der Geraden über die Achsenabschnittsform der Geraden:
\(\frac{x}{a}+\frac{y}{b}=1\).
\(\frac{x}{6,4}+\frac{y}{3,6}=1\)→\(y=-\frac{3,6}{6,4}x+3,6\)
Nun wird die x-Stelle des Standort des 2. Baumes gesucht. Sie ist \( x=6,4-4,8=1,6 \)
\(y(1,6)=-\frac{3,6}{6,4}\cdot 1,6+3,6=2,7\)
Der 2. Baum hat eine Höhe von 2,7m.