könnten sie mir eine Formel geben wie man den Anstiegswinkel berechnen kann?

Question

Aufgabe:

berechnen sie den Anstiegswinkel a von g

Problem/Ansatz:

Hallo könnten sie mir eine Formel geben wie man den Anstiegswinkel berechnen kann?

Answer 1

Sei g gegeben durch: y=mx+b, dann gilt für den Anstiegswinkel α:

m=tan(α).

Answer 2

Hallo,

frage nicht nach der Formel, sondern versuche zu verstehen, wie man zu der Formel kommt! Mal angenommen, da sind zwei Punkte $P(-1,5|\,0)$ und $Q(1,5|\,-6)$ und Du sollst den Winkel $\alpha$ der Geraden bestimmen, die durch diese beiden Punkte verläuft.

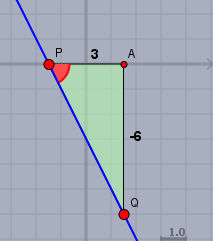
Wenn man durch beide Punkte eine vertikale und eine horizontale Gerade zieht, ergänzt man die Strecke $PQ$ zu einem rechtwinkligen Dreieck. Dies ist das sogenannte Steigungsdreieck. 'Steigungsdreieck' deshalb, weil sich daraus die Steigung $m$ der Geraden $g$ (blau) berechnen lässt. Die Steigung ist das Verhältnis aus der vertikalen zur horizontalen Differenz der Punkte - also:$$m = \frac{q_y-p_y}{q_x-p_x} = \frac{-6 - 0}{1,5 - (-1,5)} = \frac{-6}{3} = -2$$Für den Tangens des Winkels $\alpha$ (rot) gilt:$$\tan(\alpha) = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{q_y-p_y}{q_x-p_x} =m$$Also ist $\alpha$$$\alpha = \arctan(m) = \arctan(-2) \approx -63,4°$$Bem.: man schreibt $\arctan$ auch als $\tan^{-1}$. Das ist dasselbe; nur in einer anderen Schreibweise.