Hallo,
am besten machst du dir erst einmal eine Skizze:
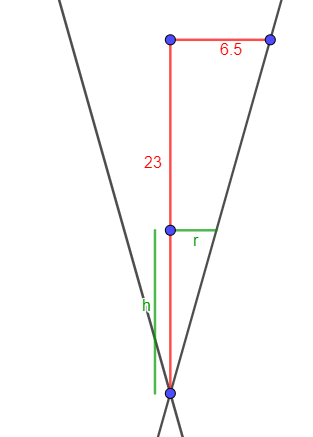
und betrachtest die rechte Seite des Querschnitts vom Messbecher.
Nach dem 2. Strahlensatz gilt:
\(\frac{r}{6,5}=\frac{h}{23}\)
Diese Gleichung kannst du nach r auflösen, indem du auf beiden Seiten mit 6,5 multiplizierst:
\(r=\frac{6,5h}{23}\)
Die rechte Seite der Gleichung setzt du in die Volumenformel des Kegels für r ein:
\(V=\frac{1}{3}\cdot \pi\cdot \bigg(\frac{6,5h}{23}\bigg)^2\cdot h\)
Das Volumen kennst du, also
\(100=\frac{1}{3}\cdot \pi\cdot \bigg(\frac{6,5h}{23}\bigg)^2\cdot h\)
Jetzt formst du um:
\( 100=\frac{1}{3}\cdot \pi\cdot \frac{40,25h^2}{529}\cdot h\\ 100=\frac{1}{3}\cdot \pi\cdot \frac{40,25h^3}{529}\\ 100=\frac{1}{3}\cdot \pi\cdot \frac{40,25}{529}\cdot h^3\\ 95,49=\frac{40,25}{529}\cdot h^3\\ 1195,60=h^3\\10,61=h\)
Ist es jetzt klarer?
Gruß, Silvia