Zeige mithilfe einer Skizze, dass es zwei Ergebnisse für die Größe des Winkels β gibt.

Question

Aufgabe:In einem dritten Dreieck ABC sind folgende Größen bekannt: AC=13,6cm; BC=8,5cm; α=24°
Justus berechnet die Größe des Winkels β = 40,6°.
d) Zeige mithilfe einer Skizze, dass es zwei Ergebnisse für die Größe des Winkels β gibt.

Answer 1

Hallo Lena,

konstruiere das Dreieck, indem Du eine Gerade $c$ zeichnest, dort den Punkt $A$ markierst, anschließend den Winkel $\alpha=24°$ und die Strecke $|AC|=13,6\,\text{cm}$ auf dem Schenkel des Winkels abträgst und einen Kreis um $C$ mit dem Radius $|BC|=8,5\,\text{cm}$ zeichnest:

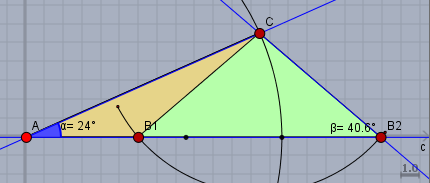
dieser Kreis um $C$ schneidet die Gerade $c$ zweimal in $B_1$ und $B_2$. Und somit erhältst Du auch zwei Dreiecke $\triangle AB_1C$ und $\triangle AB_2C$ als Lösung.

Die Berechnung von $\beta$ kann über den Sinussatz geschehen. Es gilt$$\frac{\sin \beta}{b=|AC|} = \frac{\sin \alpha }{a=|BC|}$$Somit ist $$\sin \beta = \frac{\sin \alpha \cdot |AC|}{|BC|} = \frac{\sin(24°) \cdot 13,6\,\text{cm}}{8,5\,\text{cm}} \approx 0,6508$$Für $\sin \beta = 0,6508$ hat aber $\beta$ zwei Lösungen. Nämlich$$\beta_2 = 40,6°, \quad \beta_1 = 180°-\beta_2 = 139,4°$$Weil für jeden Wert von $\beta$ gilt$$\sin(\beta) = \sin(180°-\beta)$$Gruß Werner