f ist eine auf \mathbb{R} definierte differenzierbare Funktion und die Steigung der Sekante des Graphen von f durch …

Question

Text erkannt:

(b) \( f \) ist eine auf \( \mathbb{R} \) definierte differenzierbare Funktion und die Steigung der Sekante des Graphen von \( f \) durch die Punkte \( \left(x_{0} ; f\left(x_{0}\right)\right) \) und \( \left(x_{0}+h ; f\left(x_{0}+h\right)\right) \) hat den Wert \( x_{0}+h \), für alle \( h \neq 0 \) Welche Steigung hat dann die Tangente an \( f \) in \( \left(x_{0} ; f\left(x_{0}\right)\right) \) ?
\begin{tabular}{|l|l|}
\hline 0 & \( x_{0} \) \\
\hline 0 & \( x_{0}+h \) \\
\hline 0 & \( \infty \)
\end{tabular}

Problem: Ich weiß gar nicht wo ich da anfangen soll, macht man das über die h - Methode? Könnte jemand einen Ansatz und die Lösung geben, damit ich das ausrechnen kann.

Answer 1

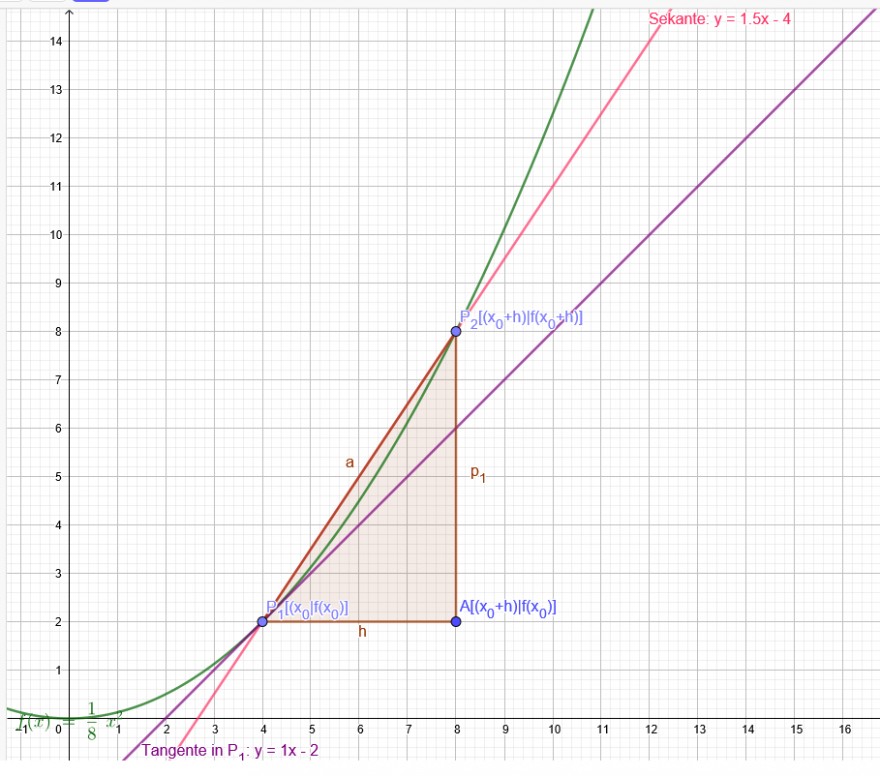
Sekantensteigung:

m=\( \frac{f(x₀+h)-f_(x₀)}{x₀+h-x₀} \)

Parabel:

f(x)=\( \frac{1}{8} \)\( x^{2} \)

Sekantensteigung:

x₀=4   f(4)=2         h=4      x₀+h=4+4=8    f(8)=8

m=\( \frac{8-2}{4+4-4} \)=\( \frac{6}{4} \)=\( \frac{3}{2} \)  Hier siehst du, dass h≠0 nötig ist.

"Welche Steigung hat dann die Tangente an \( f \) in \( \left(x_{0} ; f\left(x_{0}\right)\right) \) ?"

Hier musst du nun eine Grenzwertbetrachtung durchführen: (h-Methode)

\( m=\lim \limits_{h \rightarrow 0} \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h} \)
\( m=\lim \limits_{h \rightarrow 0} \frac{\frac{1}{8} \cdot\left(x_{0}+h\right)^{2}-\frac{1}{8} \cdot x_{0}^{2}}{h}=\lim \limits_{h \rightarrow 0} \frac{1}{8} \cdot \frac{\left(x_{0}^{2}+2 x_{0} \cdot h+h^{2}\right)-x_{0}^{2}}{h}= \)
\( =\lim \limits_{h \rightarrow 0} \frac{1}{8} \cdot \frac{2 x_{0} \cdot h+h^{2}}{h}=\lim \limits_{h \rightarrow 0} \frac{1}{8} \cdot\left(2 x_{0}+h\right) \rightarrow \frac{2}{8} \cdot x_{0}=\frac{1}{4} x_{0} \)
Für \( x_{0}=4 \) gibt es \( m=1 \)