Ok, dann kannst du den Angaben folgende Informationen entnehmen:
S (0|0) und a = 3
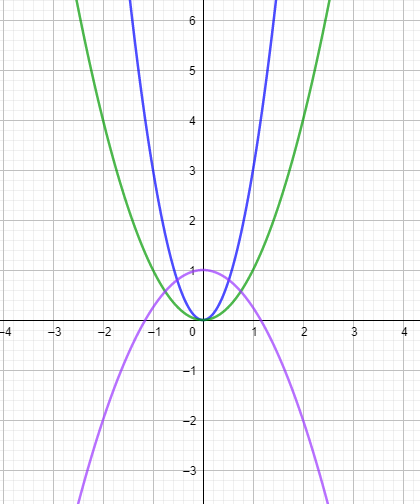
Die Normalparabel (grün) wurde nicht verschoben, aber um den Faktor 3 gestreckt (blau). Die Funktionsgleichung lautet \(y=3x^2\)
S (0|1) und a = -0,75
Die Normalparabel wurde um eine Einheit entlang der y-Achse nach oben verschoben, an der x-Achse gespiegelt und mit dem Faktor 0,75 gestaucht (lila). Die Funktionsgleichung lautet \(y=-0,75x^2+1\)
Gruß, Silvia