Also ich denke das kann nicht so ganz stimmen, könntet ihr mir weiterhelfen?

Question

Aufgabe:

eine leiter der länge 1,8 metern lehnt an einer wand. geben sie in metern auf zwei dezimalstellen gerundetan, wie weit von der wand entfernt sich das leiterende befindet, wenn das resultierende dreieck maximal groß ist.

Problem/Ansatz:

F=1/2a*b

U=a+b+c

U nach a Umstellen

a in F einsetzen

F ableiten b=-0,9

b in U einsetzen a=2,7

Also ich denke das kann nicht so ganz stimmen, könnte mir jemand bitte weiterhelfen?

Danke

Comments

Es handelt sich bei der Aufgabe um ein rechtwinkliges Dreieck.

Answer 1

Alternative:

Rechnung mit $1,80m=18dm$

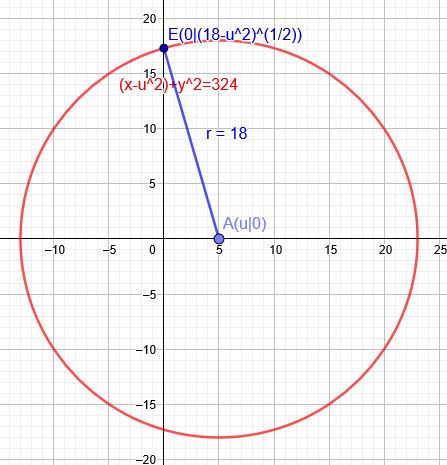
$A(u|0)$

Kreis um A mit r=18:

$(x-u)^2+y^2=18^2$

Schnitt mit der y-Achse:

$u^2+y^2=18^2$→ $y^2=18^2-u^2$→ $y=\sqrt{18^2-u^2}$ ohne Minuswert

Höhe an der Wand ist nun $h=y$

$h=\sqrt{18^2-u^2}$

Dreieckfläche:

$A(u,h)= \frac{u*h}{2}$→ $A(u)= \frac{u*\sqrt{18^2-u^2}}{2}$→ $A(u)= \frac{1}{2}*\sqrt{18^2*u^2-u^4}$

$A´(u)= \frac{-4u^3+648u}{4*\sqrt{324u^2-u^4}}=\frac{-u^3+162u}{\sqrt{324u^2-u^4}}$

$\frac{-u^3+162u}{\sqrt{324u^2-u^4}}=0$

$u^3-162u=0$ →  $u*(u^2-162)=0$  →  $u_1=0$         $u_2=\sqrt{162}≈12,73dm≈1,27m$  ohne Minuswert

$h=\sqrt{18^2-162}≈12,73dm≈1,27m$

Die größte Fläche stellt sich bei einem gleichschenklig,rechtwinkligem Dreieck ein.

Answer 2

Hallo,

du musst mit Pythagoras rechnen.

c=1,8

c²=a²+b² , also b=√(1,8²-a²)

A=0,5*a*b

A=0,5a*√(3,24-a²)

usw.

Comments

Vielen Dank für die Antwort, hat mir sehr weiter geholfen :)

---

Hattest du nicht eben noch geschrieben, du kommst nicht weiter?