Von Polynomform in die Scheitelpunktform

Question

Danke für die Antworten. Lösung ist richtig, der Link mit der Grafik jedoch falsch abgeschrieben.

Aufgabe:

Von Polynomform in die Scheitelpunktform

Problem/Ansatz:

f(x)=-2x²-3x+2

Mein Rechenweg sieht so aus

-2(x²+1.5x-1)

-2(x²+1.5x+0.56-0.56-1)

2-((x+0.75)²-1.56

-2(x+0,75)²+3.12

S(-0,75/3.12)

Habe ich mich da verrechnet?

Hier sieht der Scheitelpunkt nämlich anders aus.

Answer 1

Ich meine, dass es passt:

Plotlux öffnen

f₁(x) = -2x²-3x+2

Comments

Danke für deine Antwort.

Mir ist gerade aufgefallen, dass ich irgendwas falsches eingegeben, bzw. verändert habe und deswegen der Scheitelpunkt mir anders angezeigt wurde.

Answer 2

y = - 2·x² - 3·x + 2
y = - 2·(x² + 3/2·x) + 2
y = - 2·(x² + 3/2·x + 9/16 - 9/16) + 2
y = - 2·(x² + 3/2·x + 9/16) + 2 + 9/8
y = - 2·(x + 3/4)² + 25/8
y = - 2·(x + 0.75)² + 3.125

Deine Rechnung war also schon näherungsweise Richtig. Du solltest evtl. lernen mit Brüchen zu rechnen. Damit kann man das dann auch leicht im Kopf rechnen und braucht keine Dezimalzahlen runden.

Answer 3

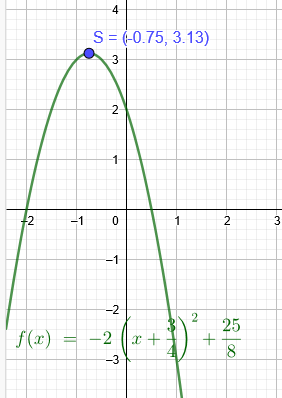
y=-2x²-3x+2|:(-2)

$\frac{y}{-2}$=x²+$\frac{3}{2}$ x-1|+1

$\frac{y}{-2}$+1=x²+$\frac{3}{2}$ x |+quadratische Ergänzung ( $\frac{3}{4}$)^2

$\frac{y}{-2}$+1+ $\frac{9}{16}$=x²+$\frac{3}{2}$ x + $\frac{9}{16}$

$\frac{y}{-2}$+ $\frac{25}{16}$=(x+$\frac{3}{4}$)^2  |*(-2)

y-$\frac{25}{8}$=-2*(x+$\frac{3}{4}$)^2  |+$\frac{25}{8}$

y=-2*(x+$\frac{3}{4}$)^2 +$\frac{25}{8}$

S(-$\frac{3}{4}$|$\frac{25}{8}$)