Berechnen sie die Schnittpunkte des Graphen von f mit der x-Achse sowie die Extrempunkte des Graphen.

Question

Aufgabe: f(x)= 5x*(2ln(x) +1)

1. Berechnen sie die Schnittpunkte des Graphen von f mit der x-Achse sowie die Extrempunkte des Graphen. Begründen sie, dass f keine wendestelle hat
2. Begründen sie, dass f(x) → 0 für x → 0 gilt

Problem/Ansatz:

Kann es jemand ausrechnen, ich mache die ganze Zeit Fehler

Answer 1

1.

Nullstellen

f(x) = 5·x·(2·LN(x) + 1) = 0

Satz vom Nullprodukt

x = 0

2·LN(x) + 1 = 0 --> x = 1/√e

Extrempunkte

f'(x) = 10·ln(x) + 15 = 0 --> x = 1/√(e^3) Nullstelle mit VZW von - zu + und damit ein Tiefpunkt

f(1/√(e^3)) = - 10/√(e^3) → TP(1/√(e^3) | - 10/√(e^3))

Wendepunkte

f''(x) = 10/x = 0 → Keine Nullstelle

2.

lim (x → 0) 5·x·(2·LN(x) + 1) = 0

Skizze

~plot~ 5*x*(2*ln(x)+1);[[0|1|-3|6]] ~plot~

Answer 2

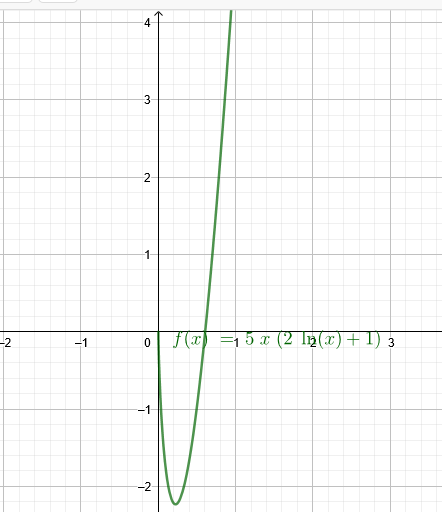
\(f(x)= 5x*(2*ln(x)+1)\)

1. Berechnen sie die Schnittpunkte des Graphen von f mit der x-Achse sowie die Extrempunkte des Graphen. Begründen sie, dass f keine wendestelle hat.

Nullstellen:

\(5x*(2*ln(x)+1)=0\)

\(x₁=0\)

\(2*ln(x)+1=0\)

\(ln(x)=-0,5\)

\( e^{ln(x)}= e^{-0,5}\)

\(x≈0,61\)

Extrempunkte des Graphen:

\(f´(x)= 5*(2*ln(x)+1)+5x*\frac{2}{x}\)

\(f´(x)= 5*(2*ln(x)+1)+10\)

\( 5*(2*ln(x)+1)+10=0\)

\( (2*ln(x)+1)=-2\)

\( (2*ln(x)+1)=-2\)

\( 2*ln(x)=-3\)

\( ln(x)=-1,5\)

\(x=e^{-1,5}≈0,223\)

 \(f(e^{-1,5})= 5*e^{-1,5}*(2*ln(e^{-1,5})+1)\)

\(f(e^{-1,5})= 5*e^{-1,5}*(-2)=-10e^{-1,5}≈-2,23\)

Art des Extremwertes über die 2. Ableitung von f(x) berechnen:

\(f´´(e^{-1,5})=\) Ist der Wert >0 dann Minimum . Bei <0 liegt ein Maximum vor.

Mit der \(f´´(x)=0\) wäre eine Wendestelle bestimmbar. Aber diese soll ja nicht da sein.