Aufgabe:
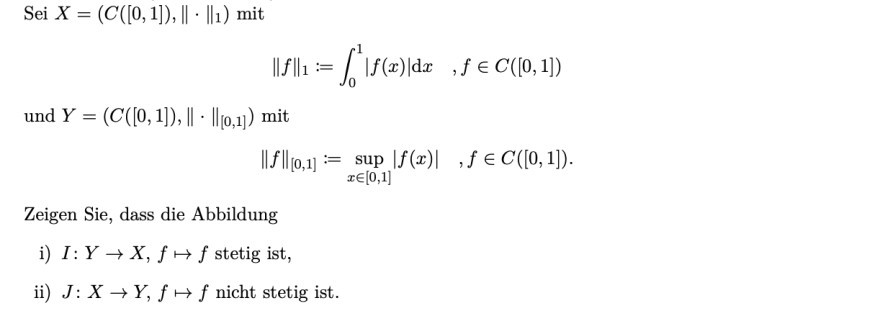
Text erkannt:
Sei \( X=\left(C([0,1]),\|\cdot\|_{1}\right) \) mit
\( \|f\|_{1}:=\int \limits_{0}^{1}|f(x)| \mathrm{d} x \quad, f \in C([0,1]) \)
und \( Y=\left(C([0,1]),\|\cdot\|_{[0,1]}\right) \) mit
\( \|f\|_{[0,1]}:=\sup _{x \in[0,1]}|f(x)| \quad, f \in C([0,1]) . \)
Zeigen Sie, dass die Abbildung
i) \( I: Y \rightarrow X, f \mapsto f \) stetig ist,
ii) \( J: X \rightarrow Y, f \mapsto f \) nicht stetig ist.
Problem/Ansatz:
Stetigkeit habe ich noch nie ganz begriffen. Wie würde man hier am besten anfangen und welches Kriterium verwenden?