Aufgabe:
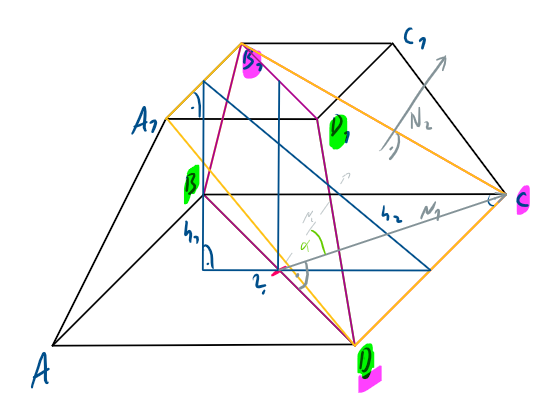
In einem regelmäßigen viereckigen Pyramidenstumpf ABCDA₁B₁C₁D₁ beträgt der Winkel zwischen den Ebenen BDD₁ und CDB₁ α. Finde das Verhältnis der Flächen der Vierecke BB₁D₁D und DA₁B₁C.
Problem/Ansatz: Diese Aufgabe habe ich von einen russischen Bekannten auf Englisch bekommen. Die Lösung soll wohl 2cos(α) sein. Allerdings komme ich auf \( \sqrt{2} \)cos(α).
Zuerst sei gesagt, dass die beiden Flächen der Vierecke jeweils auf einer der beiden Ebenen liegen, die sich mit dem Winkel α schneiden (die drei Punkte der Ebenen sind auch Ecken beim Viereck).
Die beiden Vierecke sind jeweils Trapeze. Bekanntermaßen ist der Flächeninhalt eines Trapez $$\frac{1}{2}(a+c)h$$, wobei a und c die beiden parallel liegenden Seiten sind.
Da das Verhältnis der beiden Trapeze verlangt wird, hat man die Formel sowohl im Zähler als auch im Nenner.
Dies sieht vorerst so aus:
$$\frac{\frac{1}{2}({\displaystyle {\overline {\rm {BD}}}}+{\displaystyle {\overline {\rm {B_1C_1}}}})h_1}{\frac{1}{2}({\displaystyle {\overline {\rm {CD}}}}+{\displaystyle {\overline {\rm {A_1B_1}}}})h_2}$$
Damit ein Großteil des Terms wegfallen kann, muss man allerdings die Seiten des einen Trapezes mit den Seiten des anderen Trapezes darstellen können.
Mit Hilfe des Satz des Pythagoras kann man die Strecken $${\displaystyle {\overline {\rm {BD}}}}$$ und $${\displaystyle {\overline {\rm {B_1D_1}}}}$$ folgendermaßen darstellen:
$${\displaystyle {\overline {\rm {BD}}}}=\sqrt{2} ({\displaystyle {\overline {\rm {CD}}}})$$
$${\displaystyle {\overline {\rm {B_1D_1}}}}=\sqrt{2} ({\displaystyle {\overline {\rm {A_1B_1}}}})$$
Dies kann man nun im Zähler einsetzen:
$$\frac{1}{2}(\sqrt{2}({\displaystyle {\overline {\rm {CD}}}})+\sqrt{2}({\displaystyle {\overline {\rm {A_1B_1}}}}))h_1 = \frac{1}{2}(\sqrt{2}({\displaystyle {\overline {\rm {CD}}}}+{\displaystyle {\overline {\rm {A_1B_1}}}}))h_1$$
Nun kürzt sich alles bis auf die\( \sqrt{2} \) und die beiden Höhen heraus:
$$\frac{\frac{1}{2}(\sqrt{2}({\displaystyle {\overline {\rm {CD}}}}+{\displaystyle {\overline {\rm {A_1B_1}}}}))h_1}{\frac{1}{2}({\displaystyle {\overline {\rm {CD}}}}+{\displaystyle {\overline {\rm {A_1B_1}}}})h_2} = \sqrt{2}\frac{h1}{h2}$$
Also wird nur noch das Verhältnis der beiden Höhen benötigt.
~draw~ dreieck(1|0 1|8 5|0)#~;dreieck(1|0 4|2 5|0){0F0}~;strecke(1|0 7|4);strecke(1|0 8|0);text(7|4.5 "N2");text(8|0.5 "N1");text(1.3|0.1 "α");strecke(1|0 1|9);text(1.2|9 "h1");text(2.8|5 "h2");strecke(5|0 0|10);text(4.4|0.3 "β");kreissektor(5|0 0.9 118 180 )#;kreissektor(1|0 0.9 0 34 )#;kreissektor(4|2 0.9 215 -63 )#;text(3.45|1.35 "90°");zoom(11);aus ~draw~
Skizze
Dafür schauen wir uns auch die beiden Normalenvektoren der beiden Ebenen an. Der Normalenvektor der Ebene BDD₁ zeigt, wenn man ihn auf die Grundfläche der Pyramide legt, in Richtung C.
H1 steht senkrecht auf der Grundfläche (Normalenvektor der Grundfläche) und N1 ist ein Spannvektor der Grundfläche. N2 ist der Normalenvektor der Ebene CDB₁. Zwischen N1 und N2 liegt der Winkel α (der Winkel zwischen den Ebenen). Mit H1 und H2 spannen wir nun ein Dreieck auf mit einer unbekannten Seite, die unten auf der Grundfläche der Pyramide liegt. Tragen wir nun N2 senkrecht zu H2 ein, sodass es das "Höhendreieck" an der Ecke mit dem rechten Winkel schneidet. N1 zeigt zwar nicht in die selbe Richtung wie die unbekannte Seite, liegt aber auf der selben Ebene. Daher ist auch der Winkel zwischen N2 und der unbekannten Seite bekannt (nämlich α). β ist der Winkel zwischen der unbekannten Seite (bzw. N1) und H2. Da der dritte Winkel ein rechter Winkel ist, ist β = 90° - α.
Damit ist das Verhältnis der beiden Höhen
$$\frac{h_1}{h_2}=\sin(\beta)=\sin(90°-\alpha)=\sin(\frac{\pi}{2}-\alpha)=\cos(\alpha)$$
und damit ergibt sich insgesamt:
$$\frac{\frac{1}{2}(\sqrt{2}({\displaystyle {\overline {\rm {CD}}}}+{\displaystyle {\overline {\rm {A_1B_1}}}}))h_1}{\frac{1}{2}({\displaystyle {\overline {\rm {CD}}}}+{\displaystyle {\overline {\rm {A_1B_1}}}})h_2} = \sqrt{2}\frac{h1}{h2}=\sqrt{2}\cos(\alpha)$$
Eigentlich soll das Ergebnis wohl $$2\cos(\alpha)$$ lauten. Allerdings kann ich meinen Fehler nicht finden.
Vielen Dank für eure Hilfe.
PS: Ich habe gerade gelesen, dass handschriftliche Notizen gelöscht werden. Daher bitte ich, dass zumindest die erste Skizze nicht gelöscht wird, zumal dort auch nur die Beschriftungen mit der Hand gemacht wurden und diese zum Verständnis vermutlich recht hilfreich sein kann.