Definitionsbereich und Wertebereich f(x)=x^2/(x^2+1)

Question

Hallo ich habe eine Frage bezüglich folgender Funktion.

Ich muss den Definitionsbereich und den Wertebereich bestimmen

 

f(x)=x²/(x²+1)

ich habe es mir schon im Funktionsplotter angeschaut aber mir wird einfach nicht klar wie man es berechnet.

Answer 1

Hi,

für den Definitionsbereich schaue Dir an, welche x Du einsetzen darfst. Problemstellen gibt es hier nur, wenn der Nenner 0 wird. Dieser wird nie 0, weswegen

D = ℝ

Für den Wertebereich überlege Dir was y sein kann.

Dafür würde ich schnell eine Polynomdivision machen:

x^2/(x^2+1) = 1-1/(x^2+1)

Wenn wir nun x→±∞ laufen lassen, stellen wir fest, dass das gegen 1 läuft. Erkennbar ist außerdem, dass bei x = 0 der Funktionswert 0 ist.

Daraus lässt sich die Annahme ableiten, dass für den Wertebereich gilt:

W = {ℝ|0≤y<1}

Noch ein Bild dazu zum Veranschaulichen:

 

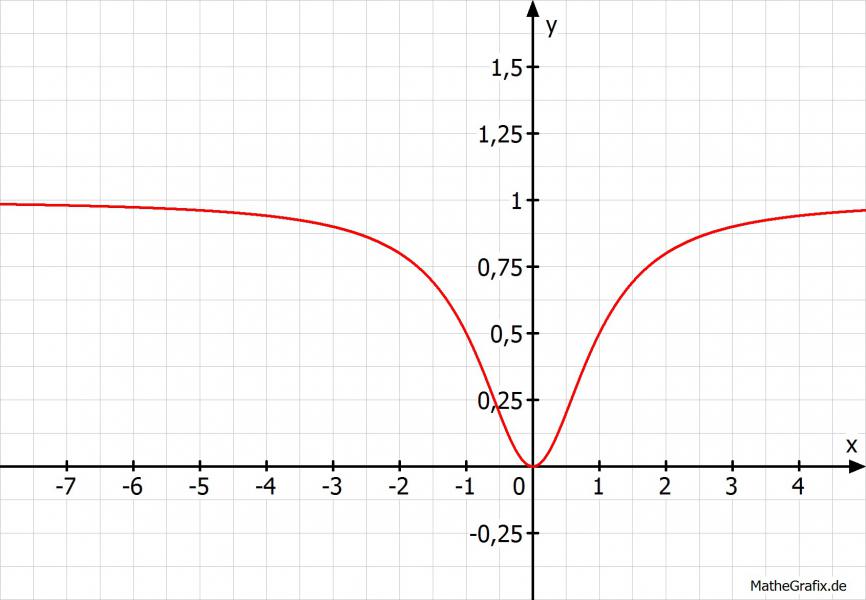
Passt also offensichtlich :).

 

Grüße

Comments

Müsste bei der Polynomdivision nicht 1+1/(x²+1) herauskommen?

---

Nope :).

(x^2          ) : (x^2 + 1)  =  1 R -1
-(x^2  + 1)
 ———
           - 1

--> 1 - 1/(x^2+1)

---

super danke,


wie kann ich bei der Funtkion denn dann erkennen ob diese injektiv, bijektiv oder surjektiv ist?

---

Injektivität besagt ja, dass jedes Element der Zielmenge nur höchstens einmal als Funktionswert angenommen wird.

Da wir eine Achsensymmetrie haben, ist das bei uns schon mal nicht der Fall.


Surjektivität besagt ja, dass jedes Element der Zielmenge (mindestens) einmal als Funktionswert angenommen wird.

Da wir aber nur zwischen 0 und 1 schwanken ist das somit nicht surjektiv (Zielmenge ist ja ℝ).


Bijektivität liegt vor, wenn obige beide zutreffen ;).

---

d.h. die funktion wäre weder injektiv noch surjektiv

---

Genau :)    .

---

ok, super das hat mir mal wieder den Sonntag gerettet, jetzt komme ich wieder vorran. Danke noch mal ;)

Answer 2

Du kannst zunächst eine Polynomdivision machen

f(x) = x^2 / (x^2 + 1) = 1 - 1/(x^2 + 1)

Definitionsbereich ist ganz R. Der Nenner wird ja nie Null sondern ist immer eine Positive Zahl größer 1.

Daraus folgt auch der Wertebereich von [0 ; 1[.