und wann kann man das nutzen, steht der Strich für konjugiert?

Question

Aufgabe:

Warum gilt

                                             

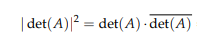
Text erkannt:

$|\operatorname{det}(A)|^{2}=\operatorname{det}(A) \cdot \overline{\operatorname{det}(A)}$

Problem/Ansatz:

und wann kann man das nutzen, steht der Strich für konjugiert? Gibt es ähnliche Regeln, die man sich merken sollte?

Würde das für ³ auch gehen?

Answer 1

Das ist keine besondere Regel.
Für jede komplexe Zahl $z$ gilt$$|z|^2=z\overline{z}$$

Answer 2

Für jede komplexe Zahl z gilt $|z^2|=z\cdot\overline{z}$. Das gilt dann natürlich auch, wenn z die Determinante einer Matrix A ist.

Answer 3

Was ist

$|a + b·i|^2$ = ...

Was ist

$(a + b·i)·(a - b·i)$ = ...