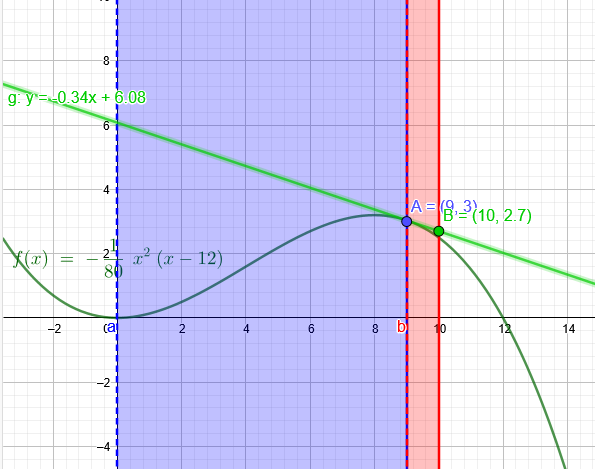
Im Bereich 0 < x ≤ 9 kann das Gestell durch eine ganzrationale Funktion dritten Grades g
beschrieben werden. Diese hat am linken Rand in P(0|0) einen Punkt mit der Steigung 0 und für
positive x-Werte ihren höchsten Punkt 8 dm weiter rechts mit der Höhe 3, 2 dm.
\(g(x)=a*x^2*(x-N)\)
höchster Punkt \(M(8|3, 2)\):
\(g(8)=64*a*(8-N)=3,2\) → \(a=\frac{1}{20*(8-N)}\)
\(g(x)=\frac{1}{20*(8-N)}*[x^2*(x-N)]\)
waagerechte Tangente in \(M(8|3, 2)\):
\(g´(x)=\frac{1}{20*(8-N)}*[2x*(x-N)+x^2*1]\)
\(g´(8)=\frac{1}{20*(8-N)}*[16*(8-N)+64]\)
\(\frac{1}{20*(8-N)}*[16*(8-N)+64=0]\)
\(N=12\)
\(g(x)=-\frac{1}{80}*[x^2*(x-12)]\)
"1.Berechnen Sie, in welcher Höhe und mit welcher Steigung dieses gerade Stück an den Graphen
von g anschließt (Funktionsgleichung von g siehe Aufgabenteil a)."
\(g(9)=-\frac{1}{80}*81*(9-12)=3,0375\)
Steigung in dem Punkt:
\(g(x)=-\frac{1}{80}*[x^2*(x-12)]=-\frac{1}{80}*(x^3-12x^2)\)
\(g´(x)=-\frac{1}{80}*(3x^2-24x)\)
\(g´(9)=-\frac{1}{80}*(3*81-24*9)=-0,3375\)
"2.Ermitteln Sie, in welcher Höhe das Geradenstück endet."
Funktion des Geradenstücks:
\( \frac{y-3,0375}{x-9}=-0,3375 \)
Wert bei \(x=10\)
\( \frac{y-3,0375}{10-9}=-0,3375 \)
\(y=3,0375-0,3375=2,7 \)