Ellipse und deren Tangente

Question

Was versteht man unter einer Tangente einer Ellipse?

Wie kann man eine Gleichung der Tangente in einem Punkt der Ellipse finden?

Bitte mit einer Zeichung erklären :/

Gib die Gleichung der Tangente im Punkt P an die Ellipse e an:

                e: x² + 5y² = 29  P(3/ y_p>0)

Answer 1

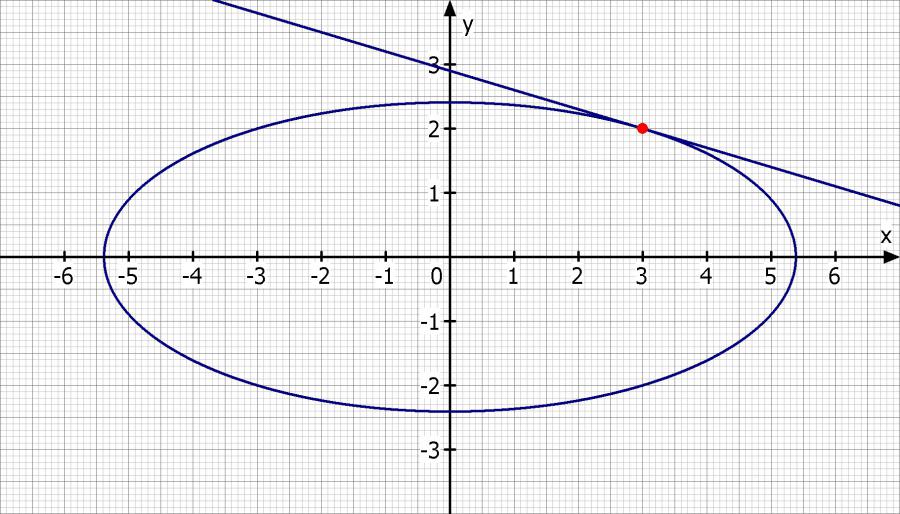
Die Tangente berührt die Ellipse in einem Punkt

x² + 5y² = 29

Zunächst x = 3 einsetzen und die y-Koordinate vom Punkt ausrechnen

3² + 5y² = 29
y = -2 ∨ y = 2

Sollte bei dir in der Klammer yp > 0 stehen dann wäre das hier 2.

Nun die Steigung im Punkt bestimmen. Ich löse die Gleichung nach y auf.

x² + 5y² = 29
y = ± √(145 - 5x²)/5 Hier brauch ich wegen yp> 0 nur die Positive Wurzel betrachten
y = √(145 - 5x²)/5

y' = - x/√(145 - 5x²)

y'(3) = - 3/√(145 - 5*3²) = -0.3

Nun die Tangente in der Punkt Steigungsform notieren

t(x) = -0.3 * (x - 3) + 2

Nun noch Ellipse und Tangente skizzieren

Answer 2

$f(x,y)=x^2 + 5y^2 - 29$

$f_x(x,y)=2x$

$f_y(x,y)=10y$

Implizite Ableitung:

$f'(x)=- \frac{2x}{10y}=- \frac{x}{5y}$   Tangente in $P(3|2)$:

$f'(3)=- \frac{3}{10}$

Punkt -Steigungsform einer Geraden:

$\frac{y-2}{x-3}= - \frac{3}{10}$

Tangente:

$y= - \frac{3}{10}x+\frac{29}{10}$