Question

Welche Anteil der Quadratfläche liegt im grauen Rechteck?

Comments

\(\displaystyle p = \underbrace{\sqrt{2^2+3^2}}_{\text{Breite}} \cdot \underbrace{4/cos(arctan(2/3))}_{\text{Länge}} \, / \, 6^2 =\frac{13}{27}\)

---

Ich habe 13/27 raus.

---

@döschwo: :-)) Tipp: multipliziere Dein Ergebnis doch mal mit 27

---

Es wäre sinnvoll, die benötigten Strecken und Winkel mit einzuzeichnen.

Das erspart, dass man das Ganze abmalen muss um eine Skizze für den

Ansatz zu haben, sowie Karl60 es gemacht hat.

---

Man kann meine Skizze nach PAINT kopieren. Winkel braucht man gar nicht.

---

Winkel braucht man gar nicht.

wohl wahr! und den Pythagoras braucht man auch nicht ;-)

---

Und man braucht auch keine gerundeten Zahlen.

---

Um ggT entgegenzukommen :
Man benötigt nur

 

Pythagoras braucht man auch nicht aber wenn man ihn hat wird die Rechtecksfläche einfach
A = a*b^2/c

Nachtrag : Einer von den Beiträgen, die man am liebsten zwei Minuten nach dem Abschicken wieder zuückziehen würde,

---

Hier findet man eine ähnliche Aufgabe

https://www.spektrum.de/raetsel/wie-viel-prozent-des-quadrats-nimmt-das-rechteck-ein/2102913

---

  

wer hier bis 7 zählen kann, ist klar im Vorteil. Vorausgesetzt, vorhandene Trigonometrie- und Analysis-Kenntnisse verstellen nicht den Blick auf das Wesentliche.

---

Ja, das ist eine Lösung ohne Winkelfunktionen und ohne Pythagoras.

Answer 1

Bezeichne die längere Seite des Rechtecks mit \(x\) und die kürzere mit \(y\). Die rechtwinkligen Dreiecke oben links und oben rechts sind zueinander ähnlich, d.h. es gilt \(\frac x4=\frac y3\) und damit$$\frac{\texttt{Rechteckfläche}}{\texttt{Quadratfläche}}=\frac{x{\cdot}y}{6^2}=\frac{\frac43y^2}{36}=\frac{\frac43(2^2{+}3^2)}{36}=\frac{13}{27}.$$

Answer 2

α=arctan\( \frac{2}{3}=33,69° \)

a=\( \sqrt{2^2+3^2}=3,601 \) a

b=\( \frac{a}{cos \alpha}=4,807 \)

a·b=17,333

das sind 48,15% der Gesamtfläche

Comments

@Karl: Das Rechnen mit Dezimalzahlen an Stelle von Brüchen ist nicht exakt 13/27≠48,15%.

Answer 3

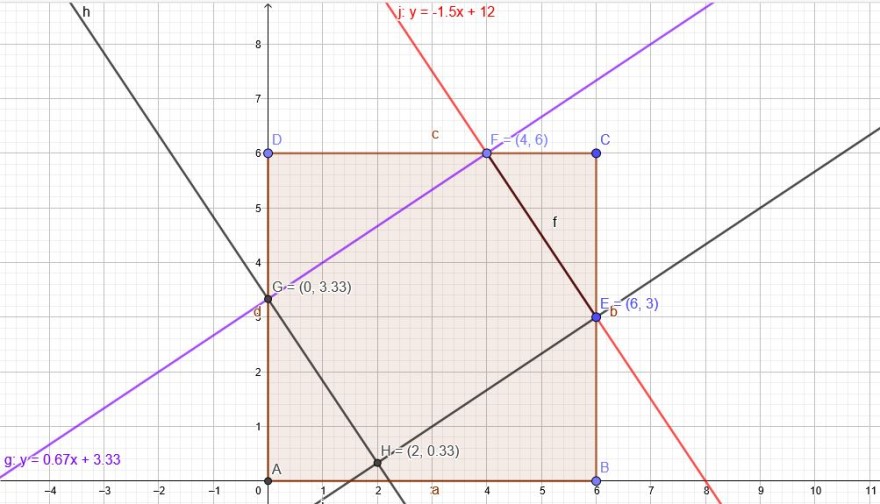
Mittels\(E(6|3)\) und \(F(4|6)\)  \(y=-1,5x+12\)

Senkrechte Gerade durch  \(F(4|6)\):

\( \frac{y-6}{x-4}=\frac{2}{3} \)  Schnitt mit y-Achse:  \( \frac{y-6}{0-4}=\frac{2}{3} \) → \( y=\frac{10}{3}\)

\(G(0|\frac{10}{3}\)
Strecke E F:\(f= \sqrt{(6-4)^2+(6-3)^2}=\sqrt{4+9}=\sqrt{13} \)

Strecke F G:\( \sqrt{(4)^2+(\frac{8}{3})^2}=\sqrt{16+\frac{64}{9}}=\sqrt{\frac{208}{9}} \)

\(A=\sqrt{13}*\sqrt{\frac{208}{9}}=\frac{1}{3}*52\)

Quadratfläche \(36\)

Rechteckfläche:  \(\frac{1}{3}*52\)

Anteil:\( \frac{\frac{1}{3}*52}{36}=\frac{52}{108}=\frac{13}{27} \)