Linearfaktorzerlegung von P2 angeben

Question

Aufgabe:

Text erkannt:

(ii) Gegeben sei das durch
$P_{2}(x):=3 x^{3}+18 x^{2}+27 x+12$
definierte Polynom $P_{2}$. Bestimmen Sie alle Nullstellen von $P_{2}$. Dabei dürfen Sie die Nullstelle $x=-1$ als gegeben annehmen. Geben Sie weiter die Vielfachheiten aller Nullstellen an, und geben Sie die Linearfaktorzerlegung von $P_{2}$ an.

Problem/Ansatz:

Ich habe die Aufgabe vollständig lösen können und habe nur eine Frage zur Linearfaktorzerlegung. Die ist in der Lösung so angegeben: Linearfaktorzerlegung: P2(x) = 3(x + 1)(x + 1)(x+4)

Meine Frage: Woher kommt die 3? Die einzelnen Faktoren sind ja die Nullstellen, aber mit der 3 davor kann ich leider gar nichts anfangen...

Answer 1

Du kannst die 3 doch als erstes ausklammern

3·x³ + 18·x² + 27·x + 12 = 3·(x³ + 6·x² + 9·x + 4)

Die Faktoren (x + 1), (x + 1), (x + 4) alleine multipliziert können ja nur x³ ohne den Faktor 3 ergeben.

Comments

Stimmt, danke.

Answer 2

Auch hier wieder: Ausklammern.

Man sieht dem Polynom ja schon von weitem an, dass man 3 ausklammern kann (alle Koeffizienten sind durch 3 (ohne Rest) teilbar).

Andersrum: Wenn Du in der Zerlegung der Lösung die 3 weglässt, wird beim Ausmultiplizieren (nicht machen, nur überlegen, was dabei passieren würde) der Term mit der höchsten Potenz $x^3$ sein, und nicht, wie es sollte, $3x^3$.

Comments

Ja du hast Recht, so sieht man es direkt. Daran hatte ich nicht gedacht. Ich glaube ich hatte sonst immer nur x³ ohne zahlen davor, deswegen war ich kurz verwirrt.

Answer 3

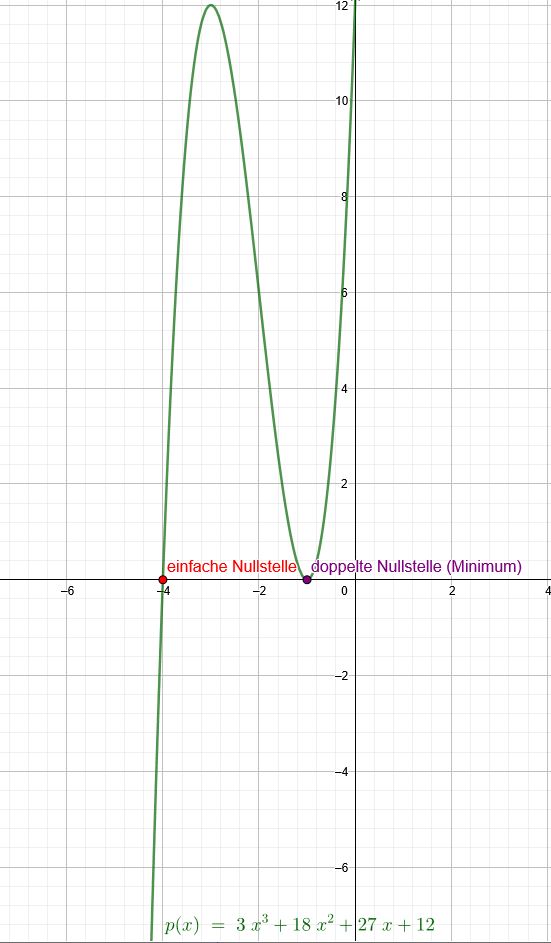
$P_{2}(x)=3 x^{3}+18 x^{2}+27 x+12$       $x=-1$ ist eine Nullstelle

Polynomdivision:

$(3 x^{3}+18 x^{2}+27 x+12):(x+1) =3x^2+15x+12$ 

$3x^2+15x+12=0$

$x^2+5x+4=0 |-4$

$x^2+5x=-4$

$(x+\frac{5}{2})^2=-4+(\frac{5}{2})^2=-4+6,25=2,25 |\sqrt{~~}$

1.)

$x+2,5=1,5$

$x_1=-1$

2.)

$x+2,5=-1,5$

$x_2=-4$

$P_{2}(x)=3 x^{3}+18 x^{2}+27 x+12=\red{3}*( x^{3}+6 x^{2}+9 x+4)$ 

$P_{2}(x)=\red{3}*(x+1)*(x+1)*(x+4)=\red{3}*(x+1)^2*(x+4)$

$x=-1$  ist eine doppelte Nullstelle (Extremwert)

$x=-4$  ist eine einfache Nullstelle

Comments

Danke dir für deine ausführliche Antwort.