Aufgabe:
Berechne den Flächeninhalt des gefärbten Dreiecks:
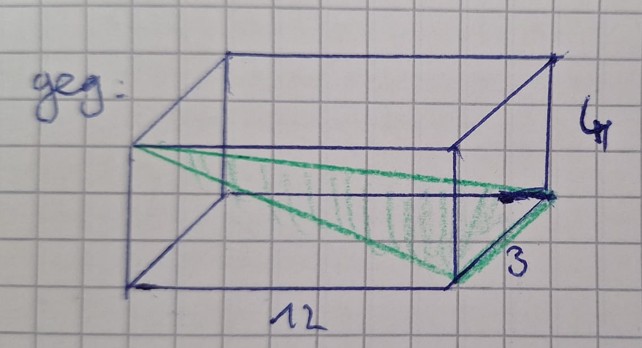
Die Skizze habe ich selbst nachgezeichnet....
Mein Ansatz:

Text:
Frontansicht von vorne:
\( \begin{aligned} d & =\sqrt{4^{2}+12^{2}} \\ d & =\sqrt{16+144} \\ d & =\sqrt{160} \\ d & =\sqrt{16 \cdot 10} \\ d & =4 \cdot \sqrt{10} \\ d & \approx 12,65 \mathrm{~cm} \end{aligned} \)
Flächeninhalt des gefärbten Dreiecks:
\( \begin{aligned} A &= \frac{1}{2} \cdot 9 \cdot h \\ A &= \frac{1}{2} \cdot 3 \cdot 4 \sqrt{10} \\ A &=18,97 \mathrm{~cm}^{2} \end{aligned} \)
Ich habe es auch mit der Vektorrechnung bestätigt:
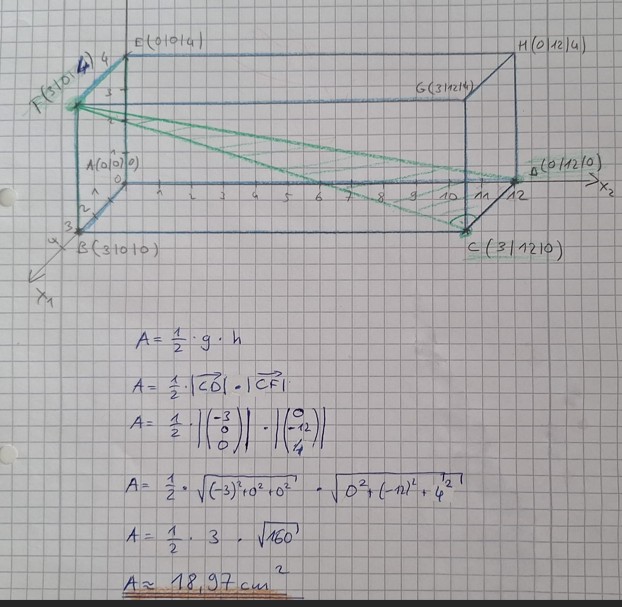
Text:
\( \begin{aligned} A &= \frac{1}{2} \cdot g \cdot h \\ A &= \frac{1}{2} \cdot\left|\overrightarrow{CD}\right| \cdot\left|\overrightarrow{CF}\right| \\ A &= \frac{1}{2} \cdot\left|\left(\begin{array}{c}-3 \\ 0 \\ 0\end{array}\right)\right| \cdot\left|\left(\begin{array}{c}0 \\ -12 \\ 4\end{array}\right)\right| \\ A &= \frac{1}{2} \cdot \sqrt{(-3)^{2}+0^{2}+0^{2}} \cdot \sqrt{0^{2}+(-12)^{2}+4^{2}} \\ A &= \frac{1}{2} \cdot 3 \cdot \sqrt{160} \\ A &\approx 18,97 \mathrm{~cm}^{2} \end{aligned} \)
Aber in der Musterlösung steht:
für die Höhe d= Wurzel aus (122 + 32) = Wurzel aus(153)......Und dann ist dort die Lösung A= 18,55 cm2
... was mit meiner Lösung nicht übereinstimmt.
Ich denke meine Lösung stimmt und die Musterlösung ist falsch. Aber vielleicht habe ich einen Denkfehler. Ich frage mich, welches die richtige Antwort ist.
Vielen Dank für eure Rückmeldung. VG