Konstruiere ein Rechteck durch 4 Punkte

Question

Auf math.stackexchange gefunden. Für Geometrieinteressierte.

Konstruiere ein Rechteck durch 4 gegebene Punkte.

Wann geht das, wann nicht?


https://math.stackexchange.com/questions/5116883/given-four-points-construct-a-rectangle-of-which-each-side-passes-through-exact

EDIT:

Let us say that 4 points are good if none of them lies in the convex hull of the other three. My intuition is that given 4 points which are good, one can always find a rectangle where each side of the rectangle passes through exactly one point.

Comments

Auf stackexchange ist das Problem anders formuliert, also ein anderes Problem als das hier genannte.

---

Geht öfter als man denkt.

Answer 1

Damit es funktioniert, müssen

(1) A,B,C,D in dieser Reihenfolge Eckpunkte eines konvexen Vierecks sein

und

(2) DA und BC einen Schnittwinkel von maximal 90° haben, wobei der Schnittpunkt von DA und BC in der Halbebene bezüglich AB liegen muss, welche C und D nicht enthält.

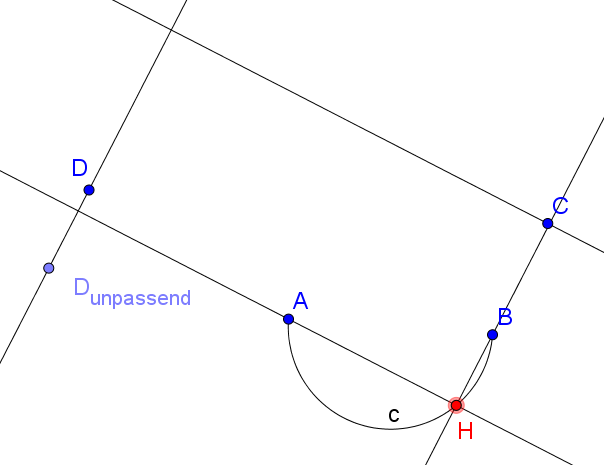
Ich habe in der Abbildung den Hilfspunkt H auf dem Thales-Halbkreis über AB so positioniert, dass C gerade noch dem Rechteck angehört. Dann gehört mein Punkt D auch dem Rechteck an, während er in der Position von D_{unpassend} außerhalb des Rechtecks liegen würde.