Suche alle Polynome 3. Grades, die durch A(-3/-7), B(-2/-4) und C(-1/3) verlaufen.

Question

Ermitteln Sie alle Funktionsgleichungen von ganzrationalen Funktionen dritten Grades, deren Graph durch die Punkte A(-3/-7), B(-2/-4) und C(-1/3) verläuft!

Answer 1

f(x) = a·x^3 + b·x^2 + c·x + d

 

f(-3) = -7
- 27·a + 9·b - 3·c + d = -7

 

f(-2) = -4
- 8·a + 4·b - 2·c + d = -4

f(-1) = 3
-a + b - c + d = 3

II' = I - II
- 19·a + 5·b - c = -3

III' = I - III
- 26·a + 8·b - 2·c = -10

 

III'' = 2II' - III'
2·b - 12·a = 4

a lass ich als Unbekannte stehen

2·b - 12·a = 4
b = 6·a + 2

 

- 19·a + 5·b - c = -3
- 19·a + 5·(6·a + 2) - c = -3
11·a - c + 10 = -3
c = 11·a + 13

-a + b - c + d = 3
-a + (6·a + 2) - (11·a + 13) + d = 3
- 6·a + d - 11 = 3
d = 6·a + 14

Damit lautet die Funktion

f(x) = a·x^3 + b·x^2 + c·x + d
f(x) = a·x^3 + (6·a + 2)·x^2 + (11·a + 13)·x + (6·a + 14)

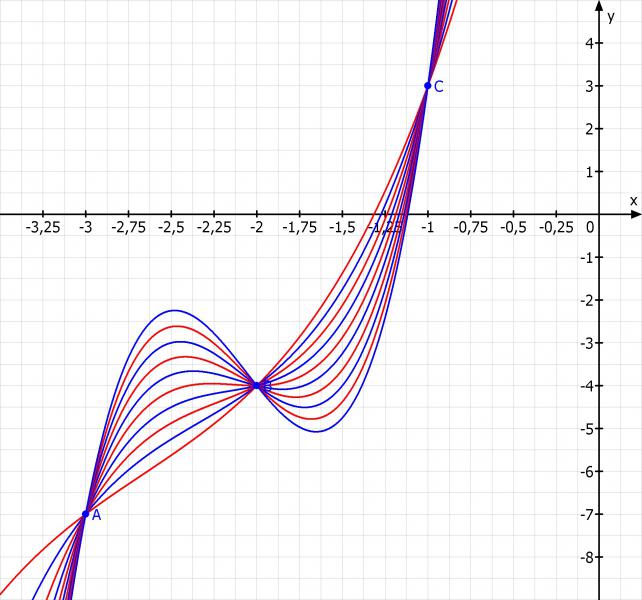
Ich skizziere die Funktion für Werte für a von 1 bis 10 in der Schrittweite 1