Könnt ihr mir bei der Bestimmung von Extrem- und Wendepunkte helfen? f(x)= 2x + √ (25-x^2)

Question

ich brauche Hilfe bei einer ´Kurvendiskussion mit Wurzelfunktion. Wir haben das noch nicht anhand einer Wurzelfunktion berechnet, aber meine alten Kentnisse zur normalen Kurvendiskussion helfen mir hier nicht weiter.

Könnt ihr mir am folgenden Beispiel helfen, dann versuch ich die restlichen vier Aufgaben alleine zu rechnen.

f(x)= 2x +√( 25-x^2)

1. Ableitungen

Habe ich mit der Kettenregel versucht: f ' = 2 - (X/wurzel (25-x^2)) Stimmt das ??

2. Symmetrie = weiß ich nicht

3. Nullstellen = Da habe ich für y= - wurzel 5 ??

4. Extrempunkte ??

5. Wendepunkte ??

Hilfeeeeee

Answer 1

1. Ableitungen

f(x) = 2·x + √(25 - x^2)
f '(x) = 2 - x/√(25 - x^2) = (2·√(25 - x^2) - x)/√(25 - x^2)
f ''(x) = - 25/(25 - x^2)^{3/2}

2. Symmetrie = weiß ich nicht

Keine erkennbare Symmetrie

3. Nullstellen = Da habe ich für y= - wurzel 5 ??

f(x) = 0
2·x + √(25 - x^2) = 0
2·x = -√(25 - x^2)
4·x^2 = 25 - x^2
5·x^2 = 25
x^2 = 5
x = ±√5

f(√5) = 4·√5
f(-√5) = 0

Damit gibt es eine Nullstelle bei -√5.

4. Extrempunkte ??

f '(x) = 0
2·√(25 - x^2) - x = 0
2·√(25 - x^2)  = x
100 - 4·x^2 = x^2
5·x^2 = 100
x^2 = 20
x = ±√20

f '(√20) = 0
f '(-√20) = 4

f(√20) = √125

5. Wendenpunkte ??

f ''(x) = 0
-25 = 0

Keinen Wendepunkt.

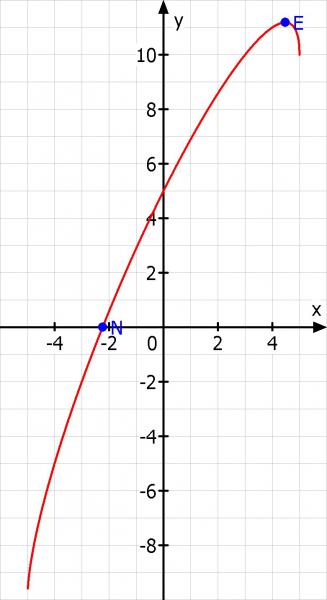
Skizze