Hi,
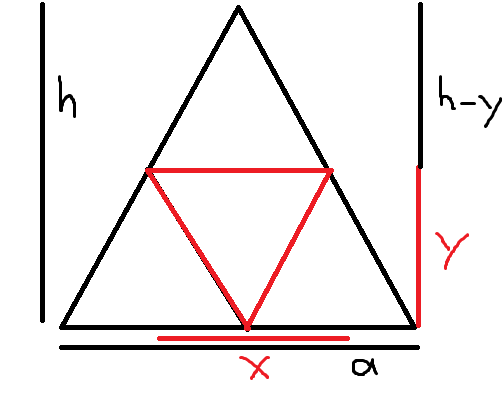
x: die Grundseite des einbeschriebenen Dreiecks
y=?: die Höhe des einbeschriebenen Dreiecks:
Zielfunktion: A(x,y)=1/2*x*y
Nebenbedingung: a/x=h/(h-y) -> ah-ay=hx -> x=(ah-ay)/h=a-(ay)/h
A(x,y)=1/2*x*y -> A(y)=1/2*(a-(ay)/h)*y=1/2*(ay-(ay²)/h)
A'(x,y) muss ja nun Null ergeben:
A'(y)=1/2*(a-(2ay)/y)=0 -> (ah-2ay)/h=0 -> ah-2ay=0 -> y=(ah)/(2a) -> y=h/2
Man muss die Grundseite des einbeschriebenen Dreiecks so einzeichnen, dass die alte Höhe h halbiert wird ;).
Und etwas Paintkünste: