Lineare Funktion durch A (-1/6) und B(3/-2), Normalparabel und Zeichnung

Question

Durch die Punkte A (-1/6) und B(3/-2) ist der Graph einer  linearen Funktion y = f(x) gegeben. Der Graph schneidet die y- Achse im Punkt C, der zugleich Scheitelpunkt einer Normalparabel ist.

a) Stelle die Funktion y = f(x) grafisch dar !

b) Gib die Gleichung der Funktion y = f(x) an.

c) Überprüfe durch Rechnung, ob der Punkt P ( 10/-16) zur Funktion y=f(x) gehört.

d) Zeichne die Normalparabel mit dem Scheitelpunkt C in das gleiche Koordinatensystem ein

e) gib die Funktionsgleichung y= g(x) der gekenzeichneten Normalparabel an

Answer 1

a) Dafür zeichnest du die beiden Punkte und verbindet sie durch eine gerade Linie. Man erhält das folgende Schaubild:

b) Für die Gleichung verwendet man die Punkt-Punkt-Form:

y - y₂ = (y₁-y₂)/(x₁-x₂) * (x-x₂)

y +2 = (6+2)/(-1-3) * (x-3)

y = -2*x + 4

 

c) Man setzt den Punkt in die Gleichung ein und prüft, ob sich eine wahre Aussage ergibt:

-16 = -2*10 + 4

-16 = -20 + 4

-16 = -16

Das ist eine wahre Aussage.

 

d) Der Schnittpunkt mit der y-Achse liegt bei x=0: C(0, 4)

 

e) Die Formel für eine Normalparabel mit dem Scheitelpunkt P(b, c) lautet:

g(x) = (x-b)² + c

also:

g(x) = x² + 4

 

Answer 2

Hi,

a) zur Zeichnung: Direkt die beiden Punkte ins Koordinatensystem einzeichnen und Gerade durchziehen:

 

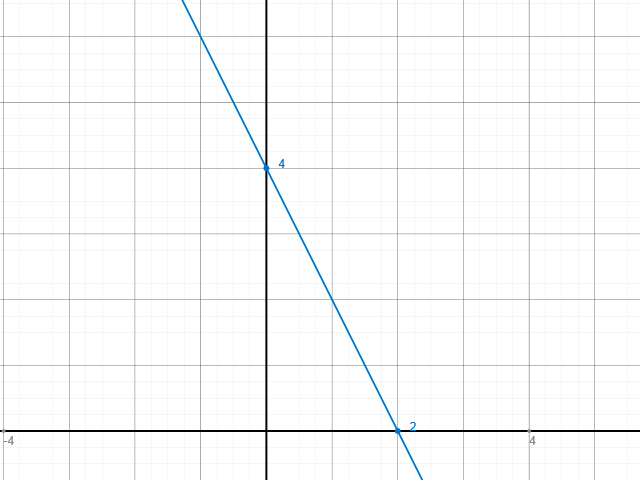
b) zur Rechnung:

Allgemeine Geradenform: y=mx+b

Zwei Gleichungen aufstellen:

6=-1*m+b

-2=3*m+b

nach b auflösen und gleichsetzen:

6+m=-2-3m    |-6+3m

4m=-8

m=-2

Damit in Gleichung 1:

6=-1*(-2)+b    |-2

4=b

 

Also: y=-2x+4

 

c) Punktprobe:

Gegeben sind y=-2x+4 und P(10|-16)

Setze x=10:

y=-2*10+4=-16

Das passt mit dem geforderten y-Wert überein. P liegt also auf der Geraden.

 

d) Parabel Zeichnung:

Lege Deine Schablone direkt auf den Schnittpunkt mit der y-Achse, bei y=4 an.

 

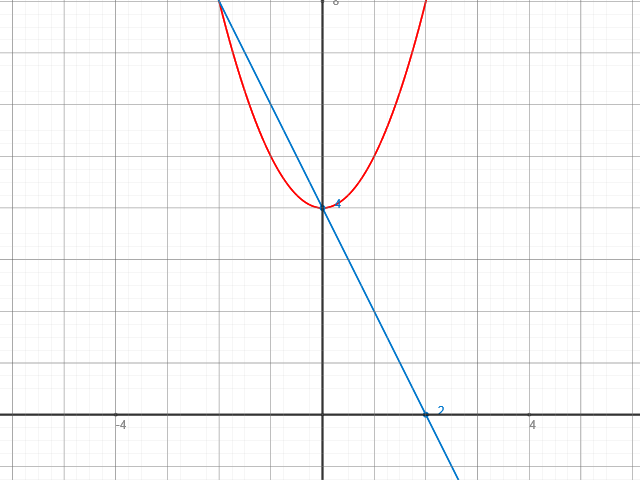
e) Angeben der Gleichung der Normalparabel

Die Normalparabel hat die Form g(x)=x²+b.

b ist dabei der y-Achsenabschnitt. Wo also der Schnittpunkt mit der y-Achse stattfindet. Das ist bei y=4 der Fall.

Demnach ist g(x)=x²+4.

 

Grüße