Nullstellen von f(x)= -4x^3 + 8x^2 - 4x durch Substitution oder Faktorisieren bestimmen

Question

f(x)= -4^3 + 8x^2 - 4x durch Faktorisieren oder Substitution? Welches kann ich wie anwenden?
EDIT (Lu): Gemeint war f(x)= -4x^3 + 8x^2 - 4x

Comments

f(x)= -4³ + 8x² - 4x

Soll es vielleicht

f(x)= -4*x³ + 8x² - 4x

heißen ?

---

Ja, tut mir Leid, ein Tippfehler.

---

Dann brauchst du doch nur x auszuklammern und hast

-4*x³ + 8x² - 4x = 0

x * ( -4*x² + 8x - 4) = 0

also x=0 oder die Klammer = 0

und letzteres gibt eine quadr. Gleichung.

Answer 1

ich sehe keinen Grund zur Substitution. Substitution wendet man nur bei geraden Exponenten an und wenn der Grad natürlich > 2 ist.

f(x)=8x²-4x-64

Jetzt einfach pq oder abc-Formel anwenden und du erhältst die Nullstellen.

LG

Answer 2

Zum leichten Faktorisieren klammere zunächst \(-4x\) aus
und wende dann die zweite binomische Formel an:

\(f(x) = -4x^3 + 8x^2 - 4x = -4x \cdot \left( x^2-2x+1 \right) = \dots \)

Danach lassen sich die beiden Nullstellen ablesen.

Answer 3

Noch ein Lösungsweg:

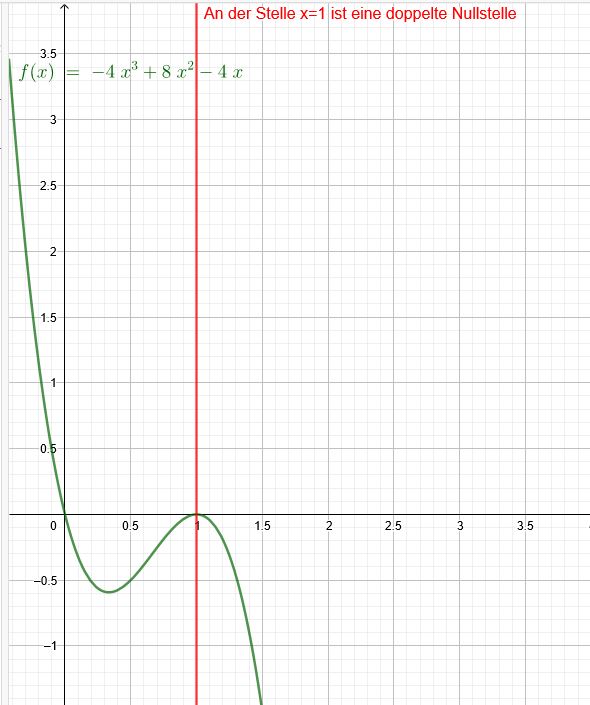
\(f(x)= -4x^3 + 8x^2 - 4x\)

\(f'(x)= -12x^2 + 16x - 4\)

\(f'(x)= -12x^2 + 16x - 4\)

\( -12x^2 + 16x - 4=0\)

\( -12x^2 + 16x =4|:(-12)\)

\( x^2 - \frac{4}{3}x =-\frac{1}{3}\)

\( x^2 - \frac{4}{3}x +(\frac{2}{3})^2=-\frac{1}{3}+(\frac{2}{3})^2=\frac{1}{9}  \)              

\( (x - \frac{2}{3})^2=\frac{1}{9} |±\sqrt{~~} \)

1.)

\( x - \frac{2}{3}=\frac{1}{3} \)

\( x_1=1 \)     \(f(1)= -4 + 8 - 4=0\) Da ist jetzt ein Extremwert (doppelte Nullstelle)

Die einfache Nullstelle ist bei \(x= 0\) entstanden durch Ausklammern von \(x\)

2.)

\( x - \frac{2}{3}=-\frac{1}{3} \)

\( x_2=\frac{1}{3} \)

Comments

Was tut/sucht man nicht alles für die Rettung der quadr. E.? :)

---

Es ist ja nicht nur die q E sondern auch, dass man mit Ableitungen eine Nullstelle finden kann( wenn man Glück hat).

---

"Da ist die quadratische Ergänzung oft eine gute Strategie:"

Schaut mal bei:

https://www.mathelounge.de/1044490/hi-wie-rechne-ich-hier-das-integral-aus