Umfang eines Vierecks in Abhängigkeit von e

Question

Aufgabe:

Gib den Umfang u des Vierecks \( A B C D \) in Abhängigkeit von \( e \) an, ohne gerundete Werte zu benutzen.

Ansatz/Problem:

Mein Ansatz ist es das Viereck in in zwei Dreiecke zu teilen (A zu C). Oben der einen bei D ist ja 60grad was muss ich nun tun ?danke im Voraus:-)

Answer 1

\( \overline{A C}=\sqrt{\left(e^{*} \sqrt{3}\right)^{2}+e^{2}}=2 e \)

Für den Winkel \( \gamma \) Beim Punkt \( C \) (im Dreieck \( A C D) \) ergibt sich:

\( \cos (\gamma)=\frac{e}{2 e}=0,5 \)

\( \rightarrow \gamma=60^{\circ} \)

Der Winkel \( \alpha \) im Dreieck \( A C D \) somit \( 30^{\circ} . \)

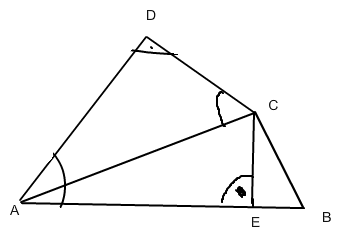
Man ergänzt den Punkt \( E \), wie in der Zeichnung.

\( \begin{array}{l} \overline{C E}=\sin \left(30^{\circ}\right) * 2 e=e \\ \overline{A E}=\sqrt{(2 e)^{2}-e^{2}}=e^{*} \sqrt{3} \\ \overline{E B}=\frac{e}{\tan \left(45^{\circ}\right)}=e \\ \overline{B C}=\sqrt{e^{2}+e^{2}}=e^{*} \sqrt{2} \\ U=e^{*} \sqrt{3}+e+e^{*} \sqrt{2}+e+e^{*} \sqrt{3} \\ U=e^{*}(2+\sqrt{2}+2 \sqrt{3)} \end{array} \)

Ich hoffe das stimmt einigermasen.