folgende Aufgabe habe ich so gelöst:
$$ Grundlage\quad Potenzgesetz\\ { x }^{ 4 }={ ({ x }^{ 2 }) }^{ 2 }\\ Aufgabe\\ 2{ x }^{ 4 }=4-{ 2x }^{ 2 }\\ Umformen\\ 2{ x }^{ 4 }=4-{ 2x }^{ 2 }\quad |-4|+{ 2x }^{ 2 }|:2\\ { x }^{ 4 }-{ x }^{ 2 }-2=0\\ Lösung\\ { x }^{ 4 }-{ x }^{ 2 }-2=0\quad |Subst.\quad Annahme:\quad z={ x }^{ 2 }\\ { z }^{ 2 }+z-2=0\quad |PQ-Formel\quad anwenden:\quad { x }_{ 1/2 }=-\frac { P }{ Q } { + }/{ - }\sqrt { (\frac { P }{ 2 } )^{ 2 }-Q } \\ \\ +\frac { 1 }{ 2 } { + }/{ - }\sqrt { (\frac { 1 }{ 2 } )^{ 2 }+2 } \Rightarrow \frac { 1 }{ 2 } { + }/{ - }\sqrt { \frac { 2 }{ 4 } +\frac { 2 }{ 1 } } \Rightarrow \frac { 1 }{ 2 } { + }/{ - }\sqrt { \frac { 2 }{ 4 } +\frac { 8 }{ 4 } } \Rightarrow \frac { 1 }{ 2 } { + }/{ - }\sqrt { \frac { 2 }{ 4 } +\frac { 8 }{ 4 } } \Rightarrow \frac { 1 }{ 2 } { + }/{ - }\sqrt { \frac { 3 }{ 2 } } \\ \\ z_{ 1 }=\frac { 1 }{ 2 } +\sqrt { \frac { 3 }{ 2 } } =1,72\\ z_{ 2 }=\frac { 1 }{ 2 } -\sqrt { \frac { 3 }{ 2 } } =-0,72\\ Umformen\quad \& \quad Resubstituieren\\ z=x^{ 2 }\quad |\sqrt { .. } \\ x=\sqrt { z } \\ \sqrt { z_{ 1/2 } } =x_{ 1/2 }\\ \sqrt { 1,72 } =\quad 1,311\quad und\quad -1,311\\ \sqrt { -0,72 } =\quad n.d.\\ Lösung\\ x_{ 1 }=1.311\quad und\quad x_{ 2 }=-1.311 $$
Wenn ich den umgeformten Ausgangsterm $$ {-2x}^{4}-{2x}^{2}+4 $$ jedoch mit Geogebra plotte, komme ich nicht auf die errechneten NST, siehe Bild: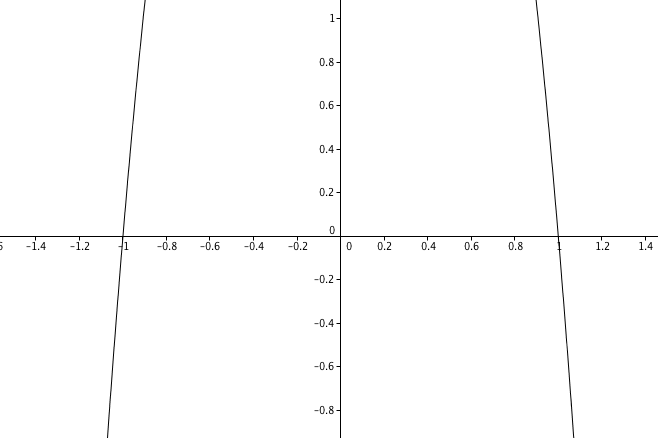
Kann es sein das ich den falschen Term zur Probe plotte ?
Grüße,
Stephan