Extremwertaufgabe Mathematik. ..., wenn möglichst wenig gegraben werden soll?

Question

Ich hab am Freitag Mathearbeit und verstehe dieses Beispiel nicht.

Von einem bestehenden Kanal g soll ein Anschluss zu zwei nebeneinader liegenden Häusern A und B gegraben werden. Um Kosten zu sparen, wird ein Teil der Strecke (in der Mitte zwischen A und B) gemeinsam gegraben. An welcher Stelle P muss die Grabung getrennt werden, wenn möglichst wenig gegraben werden soll? Wie lang ist die Grabung? (Abstand der beiden Häuser d1=24m; Abstand vom bestehenden Kanal jeweils  d2=20m.

Kann mir bitte jemand helfen ich bin am verzweifeln

Lg.

Comments

Skizze wäre vorteilhaft !

---

Ich nehme an die Sachlage ist wie folgt

Answer 1

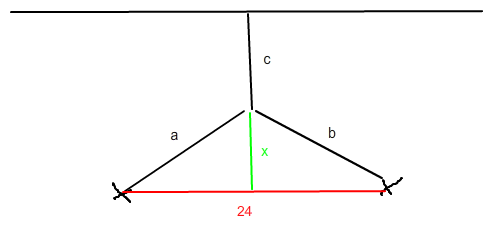
Abstand zum Kanal ist 20 also ist  c = 20 - x  und a=b = wurzel( 144 - x^2 )

Also insgesamt Grabung  f(x) = (20-x) + 2* wurzel( 144 - x^2 )

und f ' (x) = -1 +   2 / (2* wurzel( 144 - x^2 )) * (-2x)

dann ist f ' (x) = 0 , wenn 2 / (2* wurzel( 144 - x^2 )) * (-2x)  = 1

also                                 -2x = wurzel( 144 - x^2 )      quadrieren

4x^2 = 144 - x^2

x^2 = 28,8

also x= wurzel(28,8) ungefähr  5,37   Dort hat die Funktion f ihr Minimum. also

ist das der kürzeste Graben.