Abstand zweier linearer paralleler Funktionen

Question

Wir haben zwei parallele lineare Funktionen deren Abstand man bestimmen soll:

y = m*x + a --> Abstandsformel d = (m*x - y + a)/√(m^2 + 1)

y = m*x + b --> Ein Punkt (0 | b)

Setzt man den Punkt in die Abstandsformel ein erhalte ich

d = (m*0 - b + a)/√(m^2 + 1) = (a - b)/√(m^2 + 1)

Zunächst eine Frage: Ist das so richtig ?

Dann eine weitere Frage: Wie kann ich die Formel d = (a - b)/√(m^2 + 1) geometrisch deuten bzw. herleiten. 

Geht das noch schöner als über: d = (a - b) * SIN(pi/2 - ARCTAN(m))

Comments

Du gehst aus vom R^2?

 Der Abstand lässt sich dann doch einfach aus a-b = d berechnen ?

---

Nein der Abstand ist der minimale Abstand, zeichnet man diesen ein entspricht er einer Strecke die parallel zur Normalen beider Geraden ist, also senkrecht auf beiden Geraden steht.

a-b = d geht nur wenn die Geraden waagerecht sind!

Answer 1

 

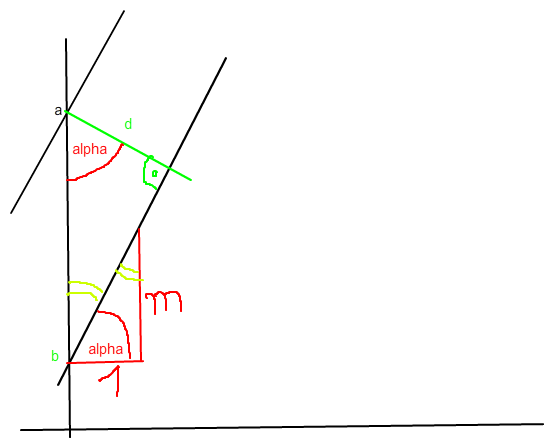
Ich hab das mal was skizziert:

Das rote ist ein Steigungsdreieck und darüber das re.wi. Dreieck enthält als eine Kathete

den Abstand d und die Hypotenuse ist a - b.

Da die gelben Winkel Wechselwinkel an Parallelen sind, sind sie gleich und damit

auch die beiden alphas.  Im Steigungsdreieck ist die Hypot, ja wurzel(1+m^2)

also ist im Steigungsdreieck cos(alpha) = 1 / wurzel(1+m^2)

und in dem anderen Dreieck cos(alpha) =d / ( a-b) 

also kannst du Gleichsetzen   1 / wurzel(1+m^2)   =   d / ( a-b)    |  * (a - b )

                                            (a - b ) /  wurzel(1+m^2)   =   d        q.e.d.