Das ist ja fast die gleiche Frage noch einmal. Ich hatte Dir doch schon gesagt, dass man
phi nur bis Pi/2 laufen lassen braucht, um "ein halbes Ei" also A/4 zu berechnen.
Also mehr und über den Weg der kartesischen Koordinaten (Wikipedia hatte ich Dir auch...):
x=r*cos(t)=sin(t)²*cos(t)
y=r*sin(t)=sin(t)²*sin(t)
90° nach rechts gekippt:
x=sin(t)²*cos(t),y=sin(t)²*sin(t) ergibt mit
inverse sin(t)²*sin(t) = asin(y^{1/3})
x(y)=sin(asin(y^{1/3}))²*cos(asin(y^{1/3})) nun x & y vertauschen, da 90° gedreht:
y= sin(asin(x^{1/3}))²*cos(asin(x^{1/3})) von 0 ... 1
sin(asin(x^{1/3}))²*cos(asin(x^{1/3})) = sqrt(1-x^{2/3}) x^{2/3}
1/4 der gesuchten Gesamtfläche beträgt also:
A/4 = ∫ sqrt(1-x^{2/3}) x^{2/3} dx, x=0...1 = 3Pi/32 = 0.294524311274...
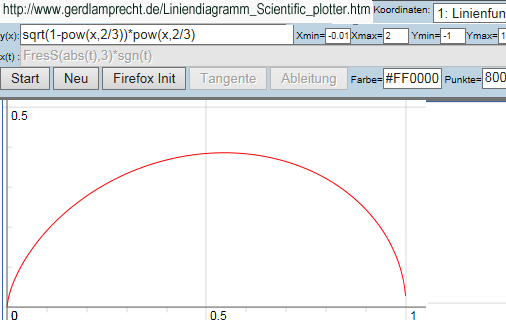
siehe Bild: sqrt(1-x^{2/3}) x^{2/3}=sqrt(1-pow(x,2/3))*pow(x,2/3)
http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
A = 4 * A/4 ... -> nun alles verstanden?