Zirkusvorführung: Aufgabe zur Funktionsbestimmung im Sachzusammenhang

Question

Hallo

Meine Aufgabe lautet:

Bei einer Zirkusvorführung wird ein Feuerball unter einem Winkel von 45 Grad aus einer "Kanone" abgeschossen und landet in einem 15m entfernten Wasserbehälter, der gegenüber der Kanonenöffnung 3,75 höher steht.

a) Bestimmen Sie eine geeignete Funktion, welche die Flugbahn des Balles beschreibt.

b) Überprüfen Sie rechnerisch, ob die Vorführung in einem 6m hohen Saal stattfinden kann.

Ich brauche Hilfe. Ich verstehe die Aufgabe gar nicht. Ich weiß nicht mal welchen Grad die Funktion haben kann :(((

Comments

Es handelt sich um einen sogenannten schrägen Wurf, der zu Schulzwecken stets unter der Annahme unvorhandener Atmosphäre zu berechnen ist, was sich durch eine Parabelfunktion modellieren lässt.

Vor Beginn tiefergehender Überlegungen ist die Anfertigung einer Skizze unabdingbar.
Skizze gemacht ?
Dann bitte zeigen.

---

Nein hab ich nicht. Ich weiß ja nicht was gemeint war. Mich Verwirrt auch die Höhe von 3,75m.

---

und landet in einem 15m entfernten Wasserbehälter, der gegenüber der Kanonenöffnung 3,75 höher steht.

Jaaa, da kann einem schon mal schwindlig werden.

und was ist da verwirrend?

Vielleicht dass sich die Manege nicht wie sonst üblich in einem Krater befindet? Tja-Matheaufgaben sind eben etwas unrealistisch ..

Answer 1

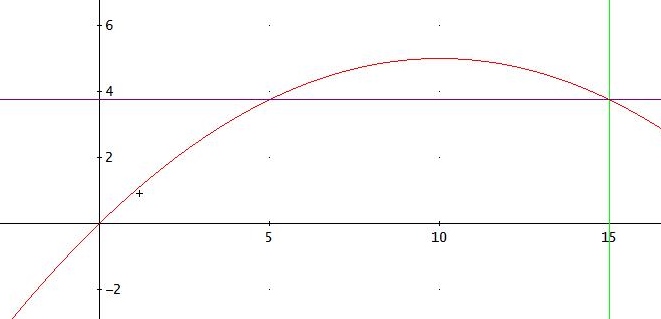
a)

Die Flugparabel hat die Gleichung  f(x) = ax² + bx + c   ->    f '(x) = 2ax + b

Wir legen das Koordinatensystem so, dass der Abschusspunkt im Nullpunkt (Ursprung) liegt.

Dann gilt:

f(0) = 0  ->  c = 0, also f(x) = ax² + bx

f '(0) = 1 weil die Tangente im Ursprung die Steigung tan(45°) = 1 hat.

->  b  = 1, also f(x) = ax² + x

f(15) = 3,75  ->  a • 15² + 15  = 3,75  ->  a = - 0,05 = - 1/20  

-> f(x) = -1/20 • x² + x ->  f '(x) = -1/10 • x + 1

b)

Für den x-Wert des höchsten Punktes [ Scheitelpunkt S(x_s|y_s)  ] gilt wegen der dort waagrechten Tangente

f ' (x_s) = 0   ->   - 1/10 • x_s + 1 = 0   ->      x_s = 10

y_s  =  f(10)  =  - 1/20 • 100 + 10  = 5    ->  S(10|5)

Der Feuerball erreicht die Maximalhöhe 5. Die Kanone kann also im Saal abgefeuert werden.

Comments

zufälliger weise habe ich die aufgabe heute auch gemacht und mir ist ein fehler aufgefallen man muss aufpassen wenn man mit 0,05 weiterrechnet da somit aus irgendwelchen unschlüssigen gründen eine komplet falsche zahl rauskommt! Deshalb sollte man mit 1/20 statt 0,005 rechnen wie dieser feine Herr.

---

Hallo mathelauch,

Die Funktion lautet
f(x) = - 0,05·x² + x
oder als Bruch
f(x) = - 1/20 *·x² + x

0.005 kommt nirgends vor:

Hast du bei deinen Rechnungen das minus
vor 0.05 beachtet ?

Soweit meine Hinweise.

---

habe den fehler schon selbst gefunden habe beim ableiten 0,5^2 gerechnet was quatsch ist den es ist 0,5*2 und ja ich meinte 0,05 habe mich vertippt :)

---

Gut.