Simplexmethode mit Textaufgabe

Question

Ein Unternhemen biete ein Futtermittelgemisch aus zwei Stoffen an. Ein Käufer benötigt bestimmte Mindestgrößen für den Nährwert der Mischung und für zwei Inahltsstoffe (=Vitamine).

Unter Berücksichtigung der Kosten 5 bzw. 6 je Mengeneinheit der beiden zu mischenden Futterstoffe ergibt sich das folgende lineare Ungleichungssystem:

Nährwert: 2x₁+ 1x₂ ≥ 6

Vitamine:  2x₁ + 4x₂ ≥ 12

                           4x₂ ≥ 4

Kosten:    5x₁ + 6x₂ --> Minimieren

Berechnen Sie bitte das optimale Mischungsverhältnis und seine Kosten.

Answer 1

Mit Hilfe sog. "Schlupfvariablen" (Hilfsvariablen) wird es möglich, das Ungleichungssystem in ein Gleichungssystem umzuwandeln. 

$$2x_1+x_2-y_1=6 \\ 2x_1+4x_2-y_2=12 \\ 4x_2-y_3=4$$ 

Jetzt müssen wir das Gleichungssystem in Tabellenform bringen: 

BV	x1	x2	y1	y2	y3	RS	Q
y1	2	1	-1	0	0	6
y2	2	4	0	-1	0	12
y3	0	4	0	0	-1	4
-K	-5	-6	0	0	0

Dann machen wir folgendes: 

1. In die Basis eintretende Variable bestimmen
2. Aus der Basis zu eliminierende Variable bestimmen
3. Basiswechsel

Eine vorliegende Lösung ist so lange nicht optimal, wie sich in der Zielfunktion (-K  Zeile) noch negative Koeffizienten befinden.

Answer 2

Hallo marianthi,

meine Überlegungen

2 * x1 + 1 * x2 ≥ 6
( x = x1, y = x2 )
ergibt die Funktion ( übliche Schreibweise )
f ( x ) ≥ 6 - 2 * x

die anderen Aussagen umgeformt
g ( x ) ≥ 3 - 1/2 * x
h ( x ) ≥ 1

Die Grafik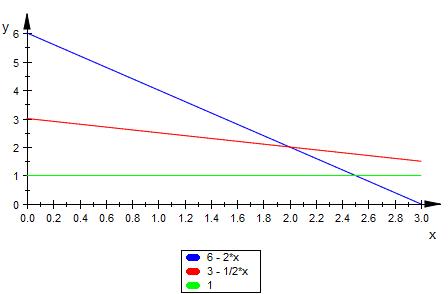
Zielgebiet
oberhalb von blau
oberhalb von rot
oberhalb von grün

Zielfunktion
5 * x1 + 6 * x2 = min
6x2 = min- 5x1
z ( x ) = min / 6 - 5/6 * x ( ocker )

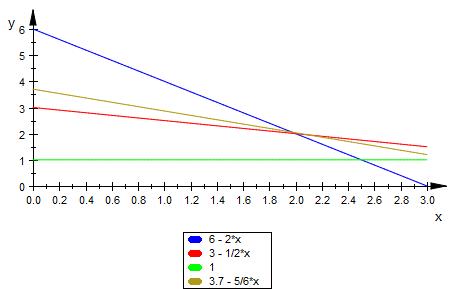
Der Schnittpunkt von blau und rot wäre der günstigste Punkt.

x1 = 2
x2 = 2

Kosten = 5x1 + 6x2 = 10 + 12 = 22

mfg Georg