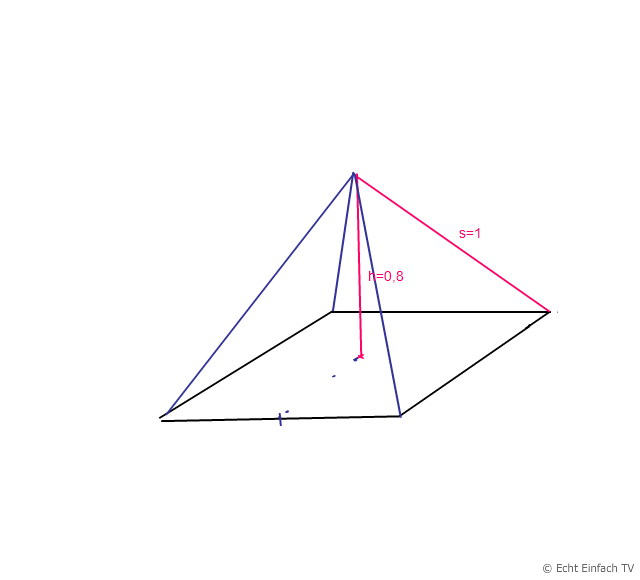
Annahme ,dass mit s=1cm nicht die Kantlänge der Pyramide gemeint ist sondern die Seitenlänge der Grundfläche.
daaus egibt sich s=a
V=(1/3)a²/h
V=1/3*1/0,8=0,2666 V=0,26666cm²
Höhe im Mantel berechnen, eine Seitenfläche der Pyramide
Pythagoras anwenden
hd=√0,5²+,08²=√0,89≅0,943
Nun den Mantel, der ja uas vier gleichschenkligen Dreiecken besteht, berechnen.
M=4*((1/2)*h*c c=s=a=1
M=4*(,05*1*0,943) =1,886 M=1,886cm²
Oberfläche ist Grundfläche und Mantel zusammen.
O = M +G G= 1*1=1cm²
O=1,886+1=2,886 O=2,886cm²
Die Aufgabenstellung war hoffentlich so zuverstehen und nicht so wie in der skizze , denn umda zu einer lösungzu kommen fehlt mindestens die Angabe eines winkels oder einer weiteren Seite.