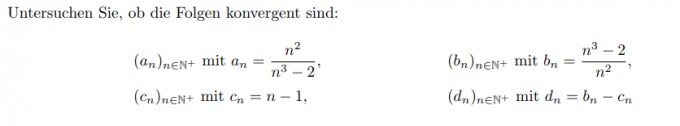Untersuchen Sie die Folgen (an), (bn), (cn) und (dn) auf Konvergenz

Question

Untersuchen Sie die Folgen (an), (bn), (cn) und (dn) mit den unten angegebenen Gliedern auf Konvergenz.

$$ { a }_{ n }=\quad \frac { { n }^{ 2 } }{ { n }^{ 3 }-2 } $$

$$ { b }_{ n }=\frac { { n }^{ 3 }-2 }{ { n }^{ 2 } } $$

$$ { c }_{ n }=n-1 $$

$$ { d }_{ n }={ b }_{ n }-{ c }_{ n } $$

Comments

Vom Duplikat:

Titel: Grenzwert Konvergenz von (dn) mit dn:= bn - cn

Stichworte: konvergenz,grenzwert,differenz,folgen

Müsste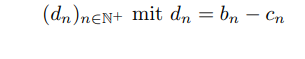 

nicht gegen 0 konvergieren, da bn  und cn abhängig voneinander sind und eine Subtraktion immer 0 ergibt ?

Ergänzung: Die komplette Aufgabe :

---

Nichts ist bekannt.

Soll auf Konvergenz überprüfen.

Sind keine weiteren Angaben vorhanden.

---

Du willst also eine Aufgabe bearbeiten, bei der eine Folge \((d_n)\), die als Differenz zweier nicht definierter Folgen definiert ist, betrachtet wird? Dies erscheint nicht sehr vielversprechend!

---

c_n und b_n stehen auf dem Zettel von

https://www.mathelounge.de/612115/monotonie-von-grenzwerten

---

Hallo dort stehen a_n und b_n kein cn

wenn es aber Wurst 21 Wurst ist, ob wir die Aufgabe kennen ist es mir auch Wurst.

 Wurst weiss anscheinend dass bn und cn voneinander abhängen, kann uns aber nichts über die 2 sagen.

lul

---

Hallo

 nein hast du nicht, dann dann kann ich sagen bn=1000 für alle n, cn=1 für alle n folgt dn=999.

soweit, wenn man nix über bn und cn weiss.

du musst wirklich die ganze Aufgabe posten, von der das ja vielleicht Teil d) ist und die bn,cn in einem anderen Teil erklärt?

lul

---

Die komplette Aufgabe .

Answer 1

Hallo

na endlich, warum nicht gleich?

da sowohl bn wie cn divergieren, kann man allgemein nichts sagen, also musst du einfach die Differenz bilden (Hauptnenner !) und dann dn untersuchen.

ich hoffe, du siehst dann, dass dn gegen 0 konvergiert.

Gruß lul

Comments

d_n strebt gegen 1

---

Hallo

dn=(-n-1)/n^2 habe ich, wie soll das gegen 1 konvergieren?

lul

---

d_n=b_n -c_n

=(n^3-2)/n^2 -(n-1)

=n-(2/n^2) -n+1

=-2/n^2 +1 ---->1

---

Hallo

 danke für die Verbesserung meines dummen Fehlers

Gruß lul

---

Gast jc2144
Wie kommst du von 
d_n=b_n -c_n
auf 
=(n3-2)/n2 -(n-1)
?

Answer 2

an = n^2 / (n^3 + 2) = 1 / (n + 2/n^2) = ...

bn = (n^3 + 2) / n^2 = (n + 2/n^2) / 1 = (n + 2/n^2) =

cn = n - 1 = ...

dn = bn - cn = n + 2/n^2 - (n - 1) = 1 + 2/n^2 = ...

Comments

Ich bin mir leider nicht sicher, ob ich verstehe, was Sie mir sagen wollen damit.

---

an habe ich mit n^2 gekürzt. Dann solltest du den Grenzwert ablesen können.

Ebenso habe ich bn gekürzt. Auch dann kann man das Verhalten für n gegen unendlich ablesen.

cn sollte ohnehin klar sein. Schreibe die Folge doch mal auf.

für dn berechnest du einfach bn - cn. Wobei du hier natürlich schon eventuell Umformungen benutzen darfst.

---

Ah ja klar!
Verzeihnung, auf den ersten Blick sah das gerade ziemlich verwirrend aus, aber wenn man es richtig aufschreibt ergibt das alles sinn. Danke für Ihre Hilfe.