Das ist mir klar. Ich meine eigentlich was anderes.
Ein anderes Beispiel:
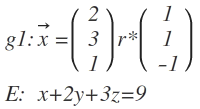
1. Lage von g1 zu E:
Koordinaten von g1:
x=2+r
y=3+r
z=1-r
Einsetzen in die Gleichung von E:
x+2y+3z=9
(2+r)+2(3+r)+3(1-r)=9
egal welchen Wert wir für r einsetzen es kommt immer heraus:
11=9
-->echt parallel
Unser Beispiel:
2x+y+z=4
2*(-1+2r)+6r+2r=4
Setzen wir r=4 ein, erhalten wir:
46=4
Setzen wir r=5 ein, erhalten wir:
58=4
das heißt verändern wir r, verändert sich die linke Seite....
also nicht echt parallel
Verstehst du was ich meine.. ich weiß aber nicht ob diese Vermutung immer zutrifft.
Das meinte ich vorhin....