Hallo MisterM,
Setze die Gleichung für die Gerade in die für den Kreis ein. man erhält
$$(x-7)^2 + (-\frac{1}{8}x + \frac{3}{2} +1)=13$$
gibt eine quadratische Gleichung
$$x^2 -14x + 49 +\frac{1}{64} x^2 - \frac{5}{8}x + \frac{25}{4}=13$$
$$\frac{65}{64}x^2-\frac{117}{8}x+\frac{169}{4}=0$$
Die Lösungen sind \(x_1=4\) und \(x_2=\frac{52}{5}\). Da es heißt: "Lichtstrahl folgt der Geraden" unterstelle ich, das der Lichtstrahl in positive X-Richtung verläuft. Demnach liegt der Punkt der Reflexion beim kleineren Wert \(x=4\).
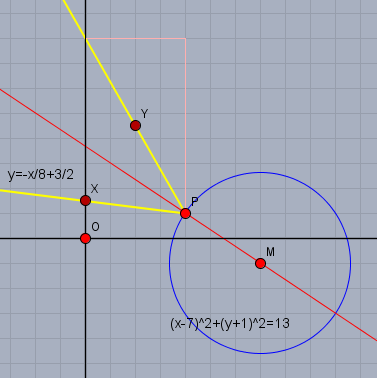
Einsetzen in die Geradengleichung ergibt den Punkt \(P\) der Reflexion \(P=(4,1)\).
Um die reflektierte Gerade zu berechnen, schwenke ich zur Vektorrechnung um. Da der Punkt \(P\) bekannt ist und \(M\) aus der Kreisgleichung folgt \(M=(7;-1)\), kann man die Reflexionsachse (rot) direkt in der Hesseschen Normalform ablesen
$$\frac{1}{\sqrt{13}}\begin{pmatrix} 2 \\ 3 \end{pmatrix} \cdot \vec{x}= \frac{1}{\sqrt{13}}\begin{pmatrix} 2 \\ 3 \end{pmatrix} \cdot P= \frac{11}{\sqrt{13}}$$ Nun wähle ich eine Punkt auf der Geraden, der nicht \(P\) ist, - z.B. \(X=(0;3/2)\) und spiegele ihn an der Reflexionsachse. Der Abstand \(e\) von der Reflexionsachse ist
$$e = \frac{1}{\sqrt{13}}\begin{pmatrix} 2 \\ 3 \end{pmatrix} \cdot X - \frac{11}{\sqrt{13}} = \frac{-13}{2 \sqrt{13}}$$
Um von \(X\) nach \(Y\) zu kommen muss man von \(X\) den Normalenvektor zweimal mit der Länge \(e\) abziehen
$$Y=X - 2e \cdot \frac{1}{\sqrt{13}}\begin{pmatrix} 2 \\ 3 \end{pmatrix}= X + \begin{pmatrix} 2 \\ 3 \end{pmatrix}=\begin{pmatrix} 2 \\ \frac{9}{2} \end{pmatrix}$$
Der reflektierte Lichtstrahl verläuft durch \(P=(4;1)\) und \(Y=(2;9/2)\) und hat somit die Funktionsgleichung
$$y=\frac{-4}{7}x+8$$
Gruß Werner