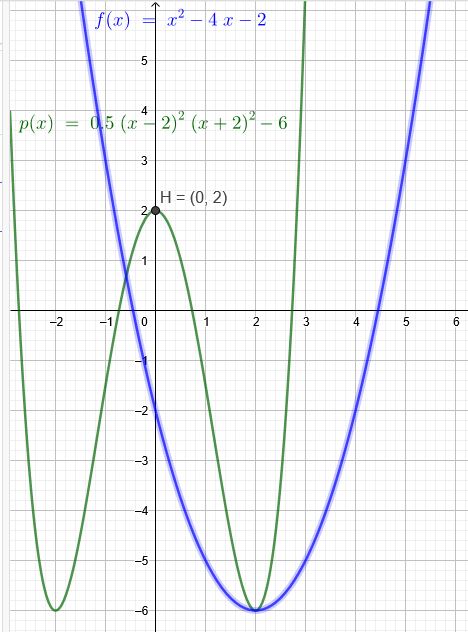
Der Graph einer zu y Achse symmetrischen Funktion 4. Grades hat im Punkt P(0|2) ein Maximum und berührt die Parabel mit der Gleichung: g(x) = x^2-4x - 2 in deren Scheitelpunkt. Berechnen sie den Scheitelpunkt von g und bestimmen sie den Funktionsterm von f
Scheitelpunkt der Parabel:
g´(x)=2x-4
2x-4=0
x=2 g(2) = 4-8 - 2=-6
S(2|-6) Hier ist nun ein Tiefpunkt von f. Da diese Parabel zur y-Achse symmetrisch ist, ist bei T(-2|-6) ein Tiefpunkt. Ich verschiebe diese beiden Tiefpunkte um 6 Einheiten nach oben. Nun sind auf der x-Achse 2 doppelte Nullstellen.
Weiter nun mit der Nullstellenform der Parabel:
f(x)=a(x-2)^2(x+2)^2
P(0|2)→P´(0|8)
f(x)=a(0-2)^2(0+2)^2=16a=8
a=0,5
f(x)=0,5(x-2)^2(x+2)^2
Nun um 6 Einheiten nach unten:
p(x)=0,5(x-2)^2(x+2)^2-6