Überprüfe die Funktion auf Randmaxima

Question

 

ich habe folgende Aufgabe: 

Untersuche eine Funktion auf Maxima und Minima in einem bestimmten Bereich (Hoch und Tiefpunkte bestimmen und auf Randmaxima überprüfen) 

Wie ich die Hoch und Tiefpunkte berechne ist mir völlig klar, aber was ist denn das Randmaximum? Und wie überprüft man das? 

Answer 1

ein ganz einfaches Beispiel, sei:
$$ f(x)=x^2 $$ mit $$ -1 < x \ \le  2 $$

Diese Funktion hat ein lokales Minimum bei \( x=0 \), und sie hat ein Maximum auf dem Rand dieses halboffenen Intervalls, und zwar \( f(2)=4 \) als größtmöglicher Funktionswert.
$$ f(x)=x^2 $$ mit $$ -1 \le  x< 2 $$ hat hingegen kein Maximum, sondern nur ein Supremum.

Comments

Sagen wir, die Aufgabe lautet so: 

f(x) 1/2x^3 - x^2 +2  -> der Intervall wäre: (-1;3) 

Zuerst berechne ich die Hoch-und Tiefpunkte

f´(x)= 3/2x^2 -2x 

f´´(x)= 3x-2 

Ich setzte die erste Ableitung gleich Null und bekomme die zwei x-Werte raus 

x1= 0 

x2= 4/3

Um zu wissen ob es ein Hoch oder Tiefpunkt ist, setzte ich es in die 2.Ableitung und bekomme die Werte raus. Dann setzte ich wieder die Nullstellen in die erste Funktion und bekomme folgendes raus. 

TP(2 / 10/9)

HP (-2/2) 

Ja und dann? 

---

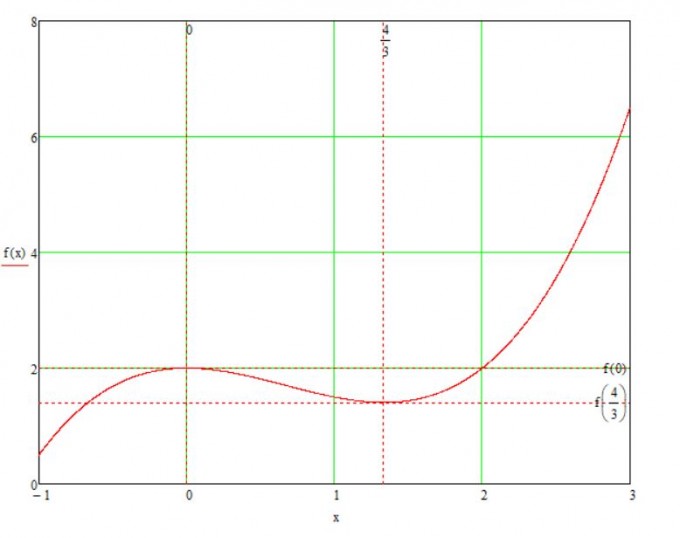
Da ist was falsch. Die kritischen Punkte sind richtig. Aber es gilt

$$ f(0) = 2 $$ und $$ f\left( \frac{4}{3} \right) = \frac{38}{27}  $$

D.h. die lokalen Extremwerte sind $$ \text{TP} = \left( \frac{4}{3} , \frac{38}{27}  \right)  $$ und

$$ \text{HP} = \left( 0 , 2  \right)  $$

Weiter gilt $$  f(-1) = \frac{1}{2} $$ und $$  f(3) = 6. $$ Damit sind beide Randpunkte Randmaximum bzw. Randminium. Das sieht man auch an der Grafik.

Answer 2

Du berechnest einfach nur die Funktionswerte am Rand.

Wenn einer größer ist, als der beim Hochpunkt , dann ist dort ein Randmaximum

entsprechend für Minimum.

Answer 3

berechne die Funktionswerte an den Rändern und schaue, ob diese kleiner/größer als die Funktionswerte bei den lokalen Minima/Maxima sind. In diesen Falle Handel es sich dann um globale Mina/Maxima.

Comments

f(x) 1/2x³ - x² +2  -> der Intervall wäre: (-1;3) 

Zuerst berechne ich die Hoch-und Tiefpunkte

f´(x)= 3/2x² -2x 

f´´(x)= 3x-2 

Ich setzte die erste Ableitung gleich Null und bekomme die zwei x-Werte raus 

x1= 0 

x2= 4/3

Um zu wissen ob es ein Hoch oder Tiefpunkt ist, setzte ich es in die 2.Ableitung und bekomme die Werte raus. Dann setzte ich wieder die Nullstellen in die erste Funktion und bekomme folgendes raus. 

TP(2 / 10/9)

HP (-2/2) 

Ja und dann? 

---

Ich habe es verstanden - danke vielmals